Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+TXĐ: X\(\in\)R
+y'=\(3x^2-6x\Rightarrow y'=0\Leftrightarrow\int_{x=2;y=0}^{x=0;y=4}\)
+y''=6(x-1)=> y' = 0 khi x = 1;y=2
+
| x | -\(\infty\) 0 1 2 +\(\infty\) |
| y' | + 0 - - 0 + |
| y |

Đáp án D
Hàm số tương đương với: y = tan 3 x − 3 tan 2 x + 1 − m tanx + 2 1
Đặt t = tanx ⇒ t ∈ 0 ; 1 → ( 1 ) y = t 3 − 3 t 2 + 1 − m t + 2
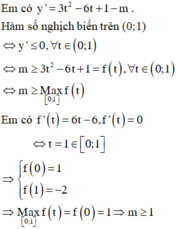

Đáp án D
Hàm số tương đương với: y = tan 3 x − 3 tan 2 x + 1 − m tanx + 2 1
Đặt t = tanx ⇒ t ∈ 0 ; 1 → ( 1 ) y = t 3 − 3 t 2 + 1 − m t + 2
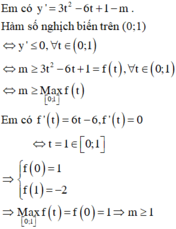

Đáp án B
Để ý thấy lời giải bài toán sai ở bước 3 do m có thể nhỏ hơn 0

Đáp án A
Phương pháp:
Xét tính đúng sai của các đáp án dựa vào các kiến thức hàm số đồng biến, nghịch biến trên khoảng xác định.
Cách giải:
*2 sai vì với c 1 < c 2 bất kỳ nằm trong a ; b ta chưa thể so sánh được f c 1 và f c 2
*3 sai. Vì y' bằng 0 tại điểm đó thì chưa chắc đã đổi dấu qua điểm đó. VD hàm số y = x 3
*4 sai: Vì thiếu điều kiện tại f ' x = 0 hữu hạn điểm.VD hàm số y = 1999 có y ' = 0 ≥ 0 nhưng là hàm hằng.
Chú ý khi giải:
HS thường nhầm lẫn:
- Khẳng định số 4 vì không chú ý đến điều kiện bằng 0 tại hữu hạn điểm.
- Khẳng định số 3 vì không chú ý đến điều kiện đổi dấu qua nghiệm.


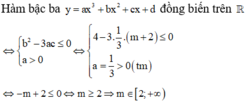

Hàm số y = - x 2 + 2 x + không nghịch biến trên ℝ ⇒ m = 0 không thỏa mãn
Để hàm số nghịch biến trên ℝ thì
Chọn: D