Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{2x+1}{x+2}\)=\(\frac{2\left(x+2\right)-3}{x+2}\)= 2 - \(\frac{3}{x+2}\)
x+2 = U(3) = {1;-1;3;-3}
xét x+2= 1 => x= - 1
x+2= -1 => x= - 3
x+2= 3 => x= 1
x+2= -3 => x= - 5
=>x= - 1 thì y= 5 => A(-1;5)
=> x= - 3 thì y = -1 => B(-3;-1)
=>x= 1 thì y = 3 => C(1;3)
=>x= - 5 thì y = 1 => D(-5;1)
=> AB giao CD tại M(-2;2)
Ta có :
n2 + n + 1 = n . ( n + 1 ) + 1
Vì n . ( n + 1 ) là tích của hai số tự nhiên liên tiếp nên ⋮2 ⇒n . ( n + 1 ) + 1 là một số lẻ nên không chia hết cho 4
Vì n . ( n + 1 ) là tích của hai số tự nhiên liên tiếp nên không có tận cùng là 4 hoặc 9. Do đó n . ( n + 1 ) + 1 không có tận cùng là 0
hoặc 5 . Vì vậy, n2 + n + 1 không chia hết cho 5
P/s đùng để ý đến câu trả lời của mình

a: 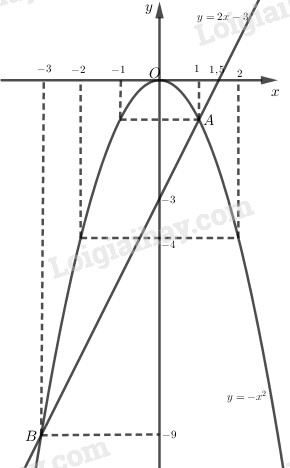
b: Phương trình hoành độ giao điểm là:
\(2x-3+x^2=0\)
=>(x+3)(x-1)=0
=>x=-3 hoặc x=1
Khi x=-3 thì y=-9
Khi x=1 thì y=-1
c: Khi x=1 và y=-1 thì \(2\cdot1-3=-1=y\)
Khi x=-3 và y=-9 thì \(2\cdot\left(-3\right)-3=-9=y\)
Khi x=1 và y=-1 thì \(-x^2=-1=y\left(nhận\right)\)
Khi x=-3 và y=-9 thì \(-x^2=-9=y\left(nhận\right)\)

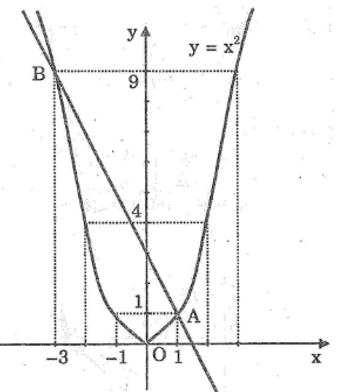
Tham khảo:


c. Giao điểm thứ hai của đồ thị có hoành độ bằng -3 và tung độ bằng 9. Ta có : B(-3 ; 9).

a) ta có pt hoành độ giao điểm: \(2x^2=x+1\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{-1}{2}\end{matrix}\right.\)
tại x= 1 thì ta có tọa độ giao điểm A(1;2)
tại x=\(\dfrac{-1}{2}\) thì ta có tọa độ giao điểm B(\(\dfrac{-1}{2};\dfrac{1}{2}\))
còn câu b) để từ từ mình suy nghĩ rồi giải sau
mình làm ra được câu b rồi
ta có pt hđgđ
\(2x^2=2mx-m-2x+2\)
\(\Leftrightarrow2x^2-\left(2m-2\right)x+\left(m-2\right)=0 \)
\(\Delta=m^2-4m+5>0\)
\(\Rightarrow X_A=\dfrac{m-1-\sqrt{m^2-4m+5}}{2};X_B=\dfrac{m-1+\sqrt{m^2-4m+5}}{2}\)
\(\Rightarrow Y_A=2\left(\dfrac{m-1-\sqrt{m^2-4m+5}}{2}\right)^2;Y_B=2\left(\dfrac{m-1+\sqrt{m^2-4m+5}}{2}\right)^2\)
1(y=2x+2)