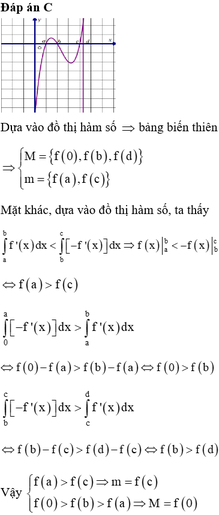Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

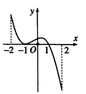
Nhận thấy trên đoạn [-2;2]
● Đồ thị hàm số có điểm thấp nhất có tọa độ (-2;-5) và (1;-5)
=> giá trị nhỏ nhất của hàm số này trên đoạn [-2;2] bằng - 5
● Đồ thị hàm số có điểm cao nhất có tọa độ (-1;1) và (-2;1)
=> giá trị lớn nhất của hàm số này trên đoạn [-2;2] bằng -1.
Chọn B.

Đáp án D
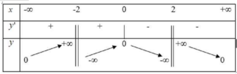
Hàm số y = f ( x ) đạt cực tiểu tại x 0 = 0
Hàm số y = f ( x ) có ba điểm cực trị.
Phương trình f ( x ) = 0 có 4 nghiệm phân biệt
Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]

Chọn C.
Phương pháp: Dựa vào bảng biến thiên để xác định tiệm cận, cực trị, giá trị lớn nhất, giá trị nhỏ nhất.
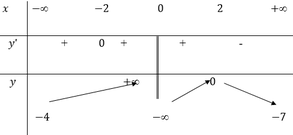
Cách giải: Dựa vào bảng biến thiên dễ thấy đồ thị hàm số có tiệm cận ngang y = 0 và hai tiệm cận đứng x = 2, x = -2. Vậy (I) sai và (IV) đúng.


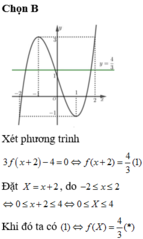
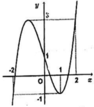
Vậy phương trình (1) có nghiệm trên đoạn [-2;2] khi và chỉ khi phương trình (*) có nghiệm trên đoạn [0;4]
Dựa vào hình vẽ ta nhận thấy trên đoạn [0;4] thì đường thẳng y = 4 3 cắt đồ thị hàm số đã cho đúng tại một điểm. Do đó phương trình (*) có đúng 1 nghiệm hay phương trình (1) có đúng một nghiệm.