Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đồ thị được vẽ như hình bên.
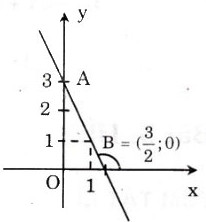
b) Gọi α là góc giữa đường thẳng y = -2x + 3 và trục Ox.
Thế thì 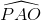 = 1800 - α.
= 1800 - α.
Ta có tg 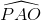 =
= 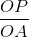 =
= 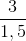 = 2.
= 2.
Suy ra 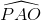 ≈ 63026’
≈ 63026’
Vậy α ≈ 116034’.
Bài giải:
a) Đồ thị được vẽ như hình bên.

b) Gọi α là góc giữa đường thẳng y = -2x + 3 và trục Ox.
Thế thì 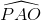 = 1800 - α.
= 1800 - α.
Ta có tg 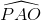 =
= 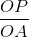 =
= 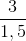 = 2.
= 2.
Suy ra 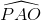 ≈ 63026’
≈ 63026’
Vậy α ≈ 116034

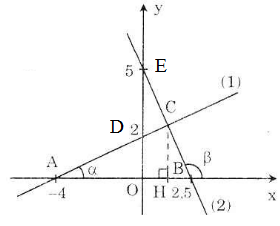
a) * Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0, tính được y = 2 => D(0; 2) thuộc đồ thị.
Cho y = 0, 0 = 0,5.x + 2 => x = -4 => A(-4; 0) thuộc đồ thị. Đường thẳng vẽ qua A, D là đồ thị của (1).
*Vẽ đồ thị hàm số y = 5 – 2x (2)
-Cho x = 0 tính được y = 5 E(0; 5) thuộc đồ thị
-Cho y = 0, 0 = 5 – 2x => x = 2,5 => B(2,5; 0) thuộc đồ thị. Đường thẳng vẽ qua B, E là đồ thị của (2).
b) Ở câu a) ta tính được tọa độ của hai điểm A và B: A(-4; 0), B(2,5; 0)

a: Vì (d)//y=1/2x+1 nên \(\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b\ne1\end{matrix}\right.\)
Vậy: (d): \(y=\dfrac{1}{2}x+b\)
Thay x=2 và y=2 vào (d), ta được:
\(b+\dfrac{1}{2}\cdot2=2\)
=>b+1=2
=>b=1
vậy: (d): \(y=\dfrac{1}{2}x+1\)
b: 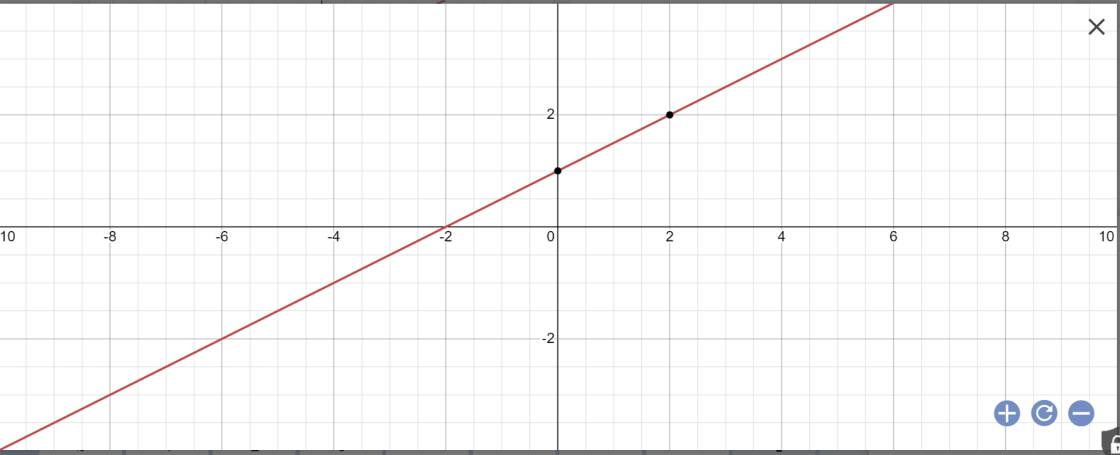
c: Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox
Ta có: (d): \(y=\dfrac{1}{2}x+1\)
=>a=1/2
=>\(tan\alpha=a=\dfrac{1}{2}\)
=>\(\alpha\simeq26^034'\)
d: tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{2}x+1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\\dfrac{1}{2}x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-2\end{matrix}\right.\)
Tọa độ C là;
\(\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}x+1=\dfrac{1}{2}\cdot0+1=1\end{matrix}\right.\)
Vậy: B(-2;0); C(1;0)
\(OB=\sqrt{\left(-2-0\right)^2+\left(0-0\right)^2}=\sqrt{2^2+0^2}=2\)
\(OC=\sqrt{\left(1-0\right)^2+\left(0-0\right)^2}=\sqrt{1^2+0^2}=1\)
Vì Ox\(\perp\)Oy nên OB\(\perp\)OC
=>ΔBOC vuông tại O
=>\(S_{BOC}=\dfrac{1}{2}\cdot OB\cdot OC=\dfrac{1}{2}\cdot2\cdot1=1\)
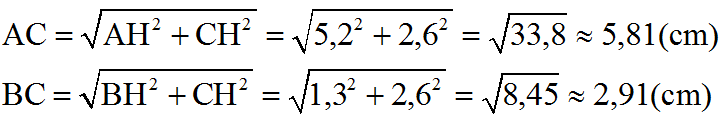


a) Vẽ đồ thị hàm số:
- Cho x = 0 thì y = 3 ta được A(0; 3)
b) Gọi góc hợp bởi đường thẳng y = -2x + 3 và trục Ox là α.