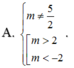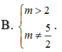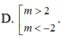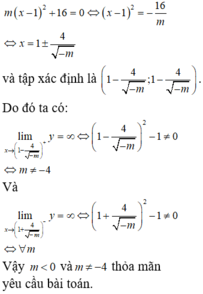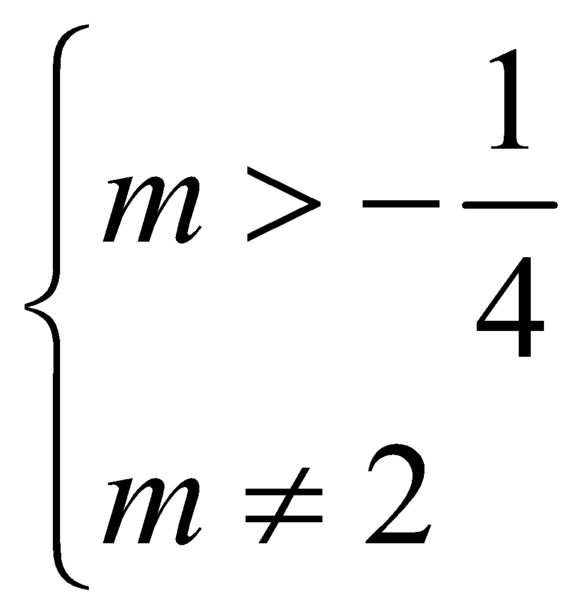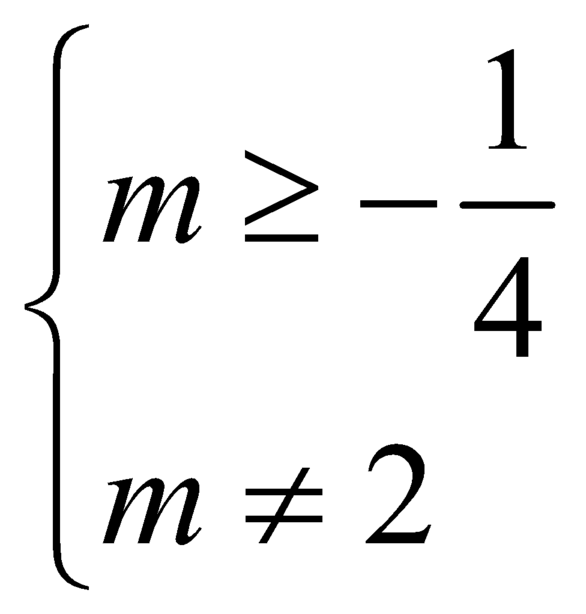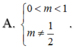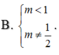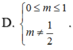Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B(Cm) có hai đường tiệm cận đứng 
có hai nghiệm phân biệt khác 1
Hàm có tiệm cận đứng khi và chỉ khi \(x^2-mx-2m^2=0\) vô nghiệm hoặc không có nghiệm \(x=2\)
\(\Rightarrow\left[{}\begin{matrix}\Delta=m^2+8m^2< 0\\4-2m-2m^2\ne0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m\ne1\\m\ne-2\end{matrix}\right.\)
Với \(m=0\) ko thỏa mãn
Với \(m\ne0\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=-\dfrac{1}{\sqrt{m}}\); \(\lim\limits_{x\rightarrow+\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=\dfrac{1}{\sqrt{m}}\)
\(\Rightarrow\) Hàm có 2 TCN khi \(\sqrt{m}\) xác định \(\Rightarrow m>0\)
Lời giải:
Để đồ thị hàm số có hai tiệm cận đứng thì phương trình $x^2-mx+1=0$ phải có hai nghiệm phân biệt khác $2$, tức là:
\(\left\{\begin{matrix} \Delta=m^2-4>0\\ f(2)=5-2m\neq 0\end{matrix}\right.\)\(\Rightarrow \begin{bmatrix} m>2\\ m<-2\end{bmatrix}\) và $m\neq\frac{5}{2}$