Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) (C) có 2 tiệm cận xiên là x = -1 và y = x + 1
I là tâm đối xứng \(\Rightarrow I\left(-1;0\right)\) (I là giao của 2 tiệm cận)
Xét \(M\left(x_0;f\left(x_0\right)\right)\in\left(C\right)\). Tiếp tuyến \(\Delta\) tại M của (C) :
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0=\frac{x_0^2+2x_0}{\left(x_0+1\right)^2}\left(x-x_0\right)+\frac{x^2_0+2x_0+2}{x_0+1}\)

a) y=x+3x+1y=x+3x+1 có tập xác định : R\{-1}
y′=−2(x+1)2<0,∀x≠−1y′=−2(x+1)2<0,∀x≠−1
Tiệm cận đứng: x = -1
Tiệm cận ngang: y = 1
Bảng biến thiên:
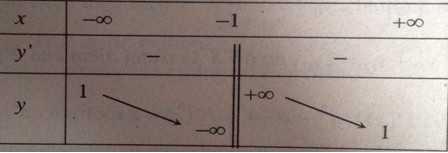
Đồ thị hàm số:
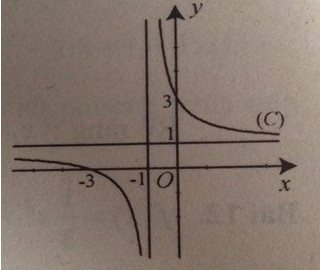
b) Xét phương trình có nghiệm là hoành độ giao điểm của (C) và đường thẳng (d): y = 2x + m
(1)
x+3x+1=2x+m⇔x+3=(2x+m)(x+1)⇔2x2+(m+1)x+m−3=0,x≠−1x+3x+1=2x+m⇔x+3=(2x+m)(x+1)⇔2x2+(m+1)x+m−3=0,x≠−1
Δ = (m+1)2 – 4.2(m-3) = m2 – 6m + 25 = (m-3)2 + 16> 0, Δm, nên (1) luôn có hai nghiệm phân biệt khác -1.
Vậy (d) luôn cắt (C) tại hai điểm phân biệt M, N (hoành độ của M, N chính là nghiệm của (1)).
TenAnh1
C = (-4.24, -6.16)
C = (-4.24, -6.16)
C = (-4.24, -6.16)
D = (11.12, -6.16)
D = (11.12, -6.16)
D = (11.12, -6.16)
E = (-4.28, -6.08)
E = (-4.28, -6.08)
E = (-4.28, -6.08)
F = (11.08, -6.08)
F = (11.08, -6.08)
F = (11.08, -6.08)
Vậy \(Min_{MN}=2\sqrt{3}\) khi \(m=3\).

a) Ta có \(\left(C\right):y=\frac{-x+2}{x+1}=-1+\frac{3}{x+1}\)
Dời hệ trục Oxy về hệ trục XIY với công thức dời trục \(\begin{cases}x=X-1\\y=Y-1\end{cases}\)
Ta có phương trình hệ trục tọa độ mới \(Y=\frac{3}{X}\),
Trong hệ trục tọa độ mới, ta giả sử \(M\left(m;\frac{3}{m}\right);N\left(n;\frac{3}{n}\right);P\left(p;\frac{3}{p}\right)\)
Gọi \(H\left(x;y\right)\) là trực tâm của tam giác MNP, ta có : \(\begin{cases}\overrightarrow{MH}.\overrightarrow{NP}=0\\\overrightarrow{NH}.\overrightarrow{MP}=0\end{cases}\) (a)
Mà \(\overrightarrow{MH}=\left(x-m;y-\frac{3}{m}\right);\overrightarrow{NP}=\left(p-n;\frac{3}{p}-\frac{3}{n}\right);\overrightarrow{NH}=\left(x-n;y-\frac{3}{n}\right);\overrightarrow{MP}=\left(p-m;\frac{3}{p}-\frac{3}{m}\right)\)
Nên (a) \(\Leftrightarrow\begin{cases}x-m-\frac{3}{np}\left(y-\frac{3}{m}\right)=0\\x-n-\frac{3}{mp}\left(y-\frac{3}{n}\right)=0\end{cases}\) \(\Leftrightarrow\begin{cases}x-\frac{3}{np}y-m+\frac{9}{mnp}=0\\x-\frac{3}{mp}y-n+\frac{9}{mnp}=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=-\frac{9}{mnp}\\y=-\frac{mnp}{3}\end{cases}\)
Suy ra \(H\left(-\frac{9}{mnp};-\frac{mnp}{3}\right)\)
Vì \(y_H=\frac{3}{x_H}\) nên \(H\in\left(C\right)\)\(\Rightarrow\) điều phải chứng minh
b) \(B\left(b;\frac{2m-b}{b+m}\right)\in\left(C_m\right)\Rightarrow\overrightarrow{AB}=\left(b;\frac{m-2b}{m+b}\right)\)
Ta có : \(I\left(-m;-1\right)\Rightarrow\overrightarrow{AI}=\left(-m;-2\right)\)
Tam giác ABI vuông cân tại A \(\Leftrightarrow\begin{cases}\overrightarrow{AB.}\overrightarrow{AI}=0\\AB^2=AI^2\end{cases}\)
\(\begin{cases}mb+2\frac{m-2b}{m+b}=0\\m^2+4=b^2+\left(\frac{m-2b}{m+b}\right)^2\end{cases}\)\(\Leftrightarrow\begin{cases}\frac{m-2b}{m+b}=-\frac{bm}{2}\left(1\right)\\m^2+4=b^2+\frac{m^2b^2}{4}\left(2\right)\end{cases}\)
\(\left(2\right)\Leftrightarrow m^2\left(b^2-4\right)+4\left(b^2-4\right)=0\Leftrightarrow\left(b^2-4\right)\left(m^2+4\right)=0\)
\(\Leftrightarrow b^2=4\Leftrightarrow b=\pm2\)
* b = 2 thay vào (1) ta được \(\frac{m-4}{m+2}=-m\Leftrightarrow m^2+3m-4=0\Leftrightarrow m=1;m=-4\)
* b = - 2 thay vào (1) ta được \(\frac{m+4}{m-2}=m\Leftrightarrow m^2-3m-4=0\Leftrightarrow m=-1;m=4\)
Vậy \(m=\pm1;m=\pm4\) là những giá trị cần tìm

Vì tam giác IAB cân tại I nên tiếp tuyến phải song song với một trong 2 đường thẳng có phương trình \(y=x;y=-x\).
Ta có \(y'=\frac{1}{\left(x+2\right)^2}>0;x\ne-2\)
Mọi \(M\left(x_0;y_0\right)\) là tiếp điểm thì \(y'\left(x_0\right)=1\Leftrightarrow1=\frac{1}{\left(x_0+2\right)^2}\Leftrightarrow\left[\begin{array}{nghiempt}x_0=-1\\x_0=-3\end{array}\right.\)
Từ đó suy ra 2 tiếp tuyến là \(y=x+1;y=x+5\)

Chọn A
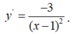
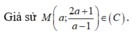
Phương trình tiếp tuyến tại điểm M là d: 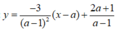
Đồ thị có hai tiệm cận có phương trình lần lượt là d 1 : x = 1; d 2 : y = 2
d cắt
d
1
tại điểm 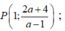
d cắt d 2 tại điểm Q(2a-1;2), d 1 cắt d 2 tại điểm I(1;2)
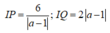
Ta có 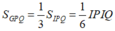
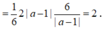

Giao điểm của đồ thị hàm số (C) và trục tung là điểm N(0;1)
Ta có : \(f'\left(x\right)=\frac{3}{\left(1-x\right)^2}\) suy ra tiếp tuyến tại điểm N là \(\left(\Delta\right):y=3x+1\Leftrightarrow\left(\Delta\right):3x-y+1=0\)
Xét điểm \(M\left(a+1;\frac{2a+3}{-a}\right)\in\left(C\right),a>0\)
Ta có : \(d_{M\\Delta }=\frac{\left|3\left(a+1\right)+\frac{2a+3}{a}+1\right|}{\sqrt{10}}=\frac{1}{\sqrt{10}}.\frac{3a^2+6a}{+3a}=\frac{3}{\sqrt{10}}\left(a+\frac{2}{a}+1\right)\ge\frac{3}{\sqrt{10}}\left(2\sqrt{2}+1\right)\)
Dấu bằng xảy ra khi \(a=\frac{2}{a}\Leftrightarrow a=\sqrt{2}\Rightarrow M\left(\sqrt{2}+1;\frac{2\sqrt{2}+5}{-\sqrt{2}}\right)\)

Phương trình hoành độ giao điểm của \(\left(\Delta_m\right)\) và \(\left(C_m\right)\) được viết thành :
\(\left(x+1\right)\left(x^2-3mx+2m^2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-m\right)\left(x-2m\right)=0\)
\(\Rightarrow\) Giao điểm của \(\left(\Delta_m\right)\) và \(\left(C_m\right)\) gồm \(A\left(-1;-m-m^2\right);B\left(m;0\right)\) và \(C\left(2m;m^2\right)\), trong số đó, A là điểm duy nhất có hoành độ không đổi (khi m thay đổi)
Đặt \(f_m\left(x\right)=x^3-\left(3m-1\right)x^2+2m\left(m-1\right)x+m^2\)
Các tiếp tuyến của \(\left(C_m\right)\) tại B và C lần lượt là các đường thẳng :
\(\left(\Delta_B\right):y=f_m'\left(x_B\right)x+y_b-f_m'\left(x_B\right)x_B\)
\(\left(\Delta_C\right):y=f_m'\left(x_C\right)x+y_C-f_m'\left(x_C\right)x_C\)
Ta cần tìm m để B và C cùng khác A và \(\Delta_B\backslash\backslash\Delta_C\), tức là :
\(\begin{cases}x_B\ne x_A\\x_C\ne x_A\\f'_m\left(x_B\right)=f'_m\left(x_C\right)\\y_B-f'_m\left(x_B\right)x_B\ne y_C-f'_m\left(x_C\right)x_C\end{cases}\)\(\Leftrightarrow\begin{cases}m\ne-1\\m\ne-\frac{1}{2}\\-m^2=2m^2+2m\\m^3\ne-4m^3-3m^2\end{cases}\)
\(\Leftrightarrow m=-\frac{2}{3}\)

Xét phương trình hoành độ giao điểm của đồ thị (C) và d :
\(\frac{2x+3}{x+2}=-2x+m\)\(\Leftrightarrow\begin{cases}x\ne-2\\2x^2+\left(6-m\right)x+3-2m=0\end{cases}\) (*)
Xét phương trình (*), ta có \(\Delta>0\), mọi \(m\in R\) và x=-2 không là nghiệm của (*) nên d luôn cắt đồ thị (C) tại 2 điểm phân biệt A, B với mọi m
Hệ số góc của tiếp tuyến tại A, tại B lần lượt là :
\(k_1=\frac{1}{\left(x_1+1\right)^2};k_2=\frac{1}{\left(x_2+1\right)^2}\) trong đó \(x_1,x_2\) là 2 nghiệm của phương trình (*)
Ta thấy :
\(k_1.k_2=\frac{1}{\left(x_1+1\right)^2.\left(x_2+1\right)^2}=\frac{1}{\left(x_1x_2+2x_1+2x_2+4\right)^2}=4\) (\(k_1>0;k_2>0\) )
Có \(P=\left(k_1\right)^{2014}+\left(k_2\right)^{2014}\ge2\sqrt{\left(k_1k_2\right)^{2014}}=2^{2015}\)
Do đó , Min \(P=2^{2015}\) đạt được khi và chỉ khi \(k_1=k_2\)
\(\Leftrightarrow\frac{1}{\left(x_1+2\right)^2}=\frac{1}{\left(x_2+2\right)^2}\Leftrightarrow\left(x_1+2\right)^2=\left(x_2+2\right)^2\)
Do \(x_1,x_2\) phân biệt nên ta có \(x_1+2=-x_2-2\)
\(\Leftrightarrow x_1+x_2=-4\Leftrightarrow m=-2\)
Vậy giá trị cần tìm là \(m=-2\)
Gọi \(M\left(x_0;y_0\right);y_0=\frac{2x_0-1}{x_0-1}\)
Phương trình tiếp tuyến \(\Delta\) của (C) tại M là :
\(y=\frac{-1}{\left(x_0-1\right)^2}\left(x-x_0+\frac{2x_0-1}{x_0-1}\right)\)
\(\Delta\) cắt tiệm cận đứng x = 1 tại A có tọa độ là nghiệm của hệ
\(\begin{cases}x=1\\y=\frac{-1}{\left(x_0-1\right)^2}\left(x-x_0+\frac{2x_0-1}{x_0-1}\right)\end{cases}\)
Do đó \(A\left(1;\frac{2x_0}{x_0-1}\right)\)