Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
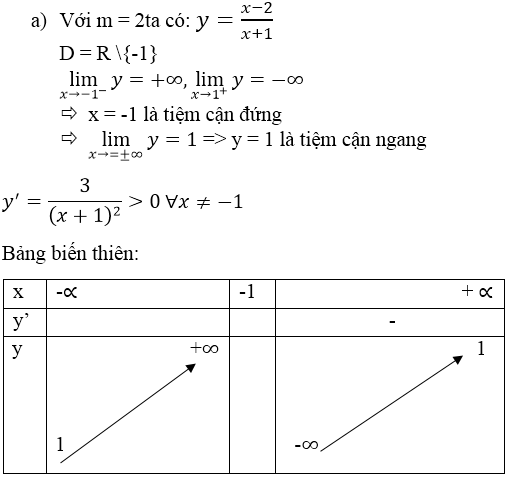
Với m = 2 ta có hàm số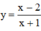 
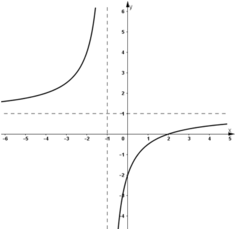
- Tập xác định : D = R\{-1}.
- Sự biến thiên :
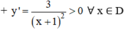
⇒ Hàm số đồng biến trên (-∞ ; -1) và (-1 ; +∞).
+ Cực trị : hàm số không có cực trị
+ Tiệm cận :
⇒ y = 1 là tiệm cận ngang của đồ thị hàm số
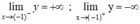
⇒ x = -1 là tiệm cận ngang của đồ thị hàm số.
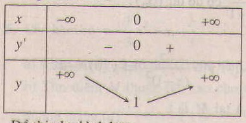
+ Bảng biến thiên :
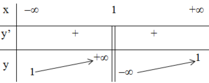
- Đồ thị :
a) Điểm (-1 ; 1) thuộc đồ thị của hàm số ⇔ .
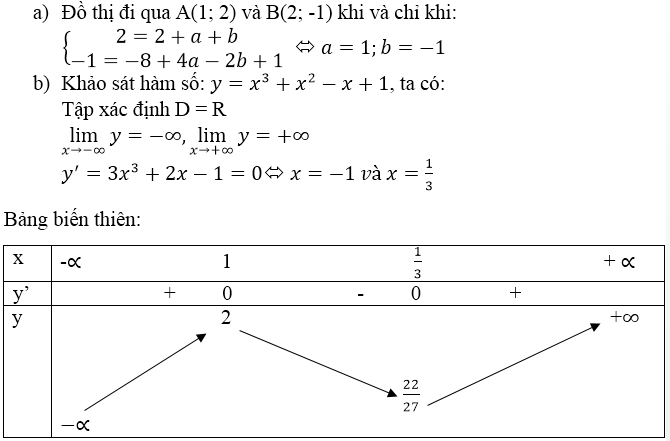
b) m = 1 . Tập xác định : R.
y' = 0 ⇔ x = 0.
Bảng biến thiên:
Đồ thị như hình bên.
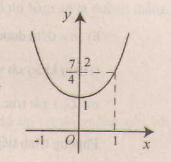
c) Vậy hai điểm thuộc (C) có tung độ
là A(1 ;
) và B(-1 ;
). Ta có y'(-1) = -2, y'(1) = 2.
Phương trình tiếp tuyến với (C) tại A là : y - = y'(1)(x - 1) ⇔ y = 2x -
Phương trình tiếp tuyến với (C) tại B là : y - = y'(-1)(x + 1) ⇔ y = -2x -
.
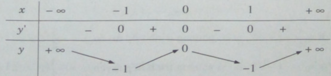
y = x 4 – 2 x 2
y′ = 4 x 3 – 4x = 4x( x 2 – 1)
y′ = 0 ⇔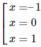 
Bảng biến thiên:
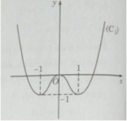
Đồ thị
. Tập xác định : R 
{
} ;
và 
;
) ∈ ∆ ⇔ 
.
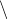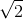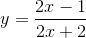Với m = 2 ta được hàm số: y = 2 x - 1 2 x + 2
- TXĐ: D = R \ {-1}
- Sự biến thiên:
+ Chiều biến thiên: Theo kết quả câu a)
Hàm số đồng biến trên (-∞ ; -1) và (-1 ; +∞)
+ Cực trị : Hàm số không có cực trị.
+ Tiệm cận:
⇒ đồ thị có tiệm cận đứng là x = -1.
Lại có
⇒ đồ thị có tiệm cận ngang là y = 1.
+ Bảng biến thiên:
- Đồ thị:
+ Đồ thị cắt trục hoành tại (1/2 ; 0).
+ Đồ thị cắt trục tung tại (0 ; -1/2).
+ Đồ thị nhận I(-1 ; 1) là tâm đối xứng.