
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

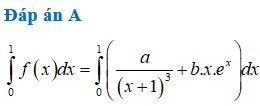
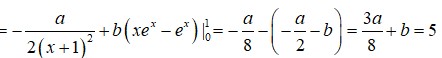
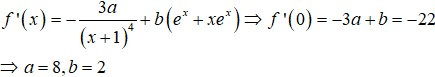

Ta có:
\(f\left(1\right).f\left(-1\right)=\left(a+b\right).\left(-a+b\right)\)
\(\Rightarrow\left(a+b\right)\left(-a+b\right)=\left(a+b\right)^2\)
\(\Rightarrow-a+b=a+b\)
\(\Rightarrow a=-a\)
\(a\ne0\) thì làm sao có a thỏa mãn được?
Trần Thùy Dung ko biết thì đừng có làm. 5 - 3a - 3b = 5. Bài này trong violympic.


⇒ ∫ 1 x f ' x 1 + f x 2 f x 4 d x = ∫ 1 x x − 1 2 d x , ∀ x ∈ 1 ; 3 ⇔ ∫ 1 x 1 f x 4 + 2 f x 3 + 1 f x 2 d f x = x − 1 3 3 x 1 ⇔ − 1 3 f x 3 − 2 2 f x 2 − 1 f x x 1 = x − 1 3 3 − 0 3 ⇔ − 1 3 f x 3 − 2 2 f x 2 − 1 f x − − 1 3 f 1 3 − 2 2 f 1 2 − 1 f 1 = x − 1 3 3 ⇔ − 1 3 f x 3 − 2 2 f x 2 − 1 f x − 1 3 − 1 + 1 = x − 1 3 3 ⇔ − 1 3 f x 3 − 2 2 f x 2 − 1 f x = x − 1 3 + 1 3 ⇔ 1 3 − 1 f x 3 − − 1 f x 2 + − 1 f x = 1 3 x 3 − x 2 + x ( * )


a/ f(x) = 0 => x2 + 4x - 5 = 0 => (x - 1)(x + 5) = 0 => x = 1 hoặc x = -5
Vậy x = 1 , x = -5
b/ f(x) > 0 => x2 + 4x - 5 > 0 => (x - 1)(x + 5) > 0 => x - 1 > 0 và x + 5 > 0 => x > 1 và x > -5 => x > 1
hoặc x - 1 < 0 và x + 5 < 0 => x < 1 và x < -5 => x < -5
Vậy x > 1 hoặc x < -5
c/ f(x) < 0 => x2 + 4x - 5 < 0 => (x - 1)(x + 5) < 0 => x - 1 > 0 và x + 5 < 0 => x > 1 và x < -5 => vô lí
hoặc x - 1 < 0 và x + 5 > 0 => x < 1 và x > -5 => -5 < x < 1
Vậy -5 < x < 1

Đáp án B
Do f 0 < 0 < f − 1 nên phương trình f x = 0 có ít nhất 1 nghiệm x ∈ − 1 ; 0
Đáp án đúng là S = ∫ − 1 1 f x d x

S là tập con của F trong các trường hợp sau:
TH1: S là tập rỗng, tức là pt x2 - 2x + m = 0 vô nghiệm => delta' = 1 - m < 0 => m > 1
TH2: S có 1 nghiệm kép < 0 => delta' = 1 - m = 0 và nghiệm kép -b'/a = 1 < 0. Điều này không xảy ra
TH3: S có 2 nghiệm đều < 0 => Tổng 2 nghiệm cũng < 0. Mà tổng 2 nghiệm = -b/a = 1 là số dương => Điều này cũng ko bao giờ xảy ra.
Vậy m > 1 thì S là rỗng và khi đó S là tập con của F.