Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điều kiện xác định: \(x\ge0\).
Lấy \(x_1>x_2\ge0\).
\(f\left(x_1\right)-f\left(x_2\right)=\sqrt{x_1}-\sqrt{x_2}=\frac{x_1-x_2}{\sqrt{x_1}+\sqrt{x_2}}>0\)
Do đó hàm số đồng biến.
Lần lượt thế tọa độ các điểm vào hàm số ban đầu, ta thấy điểm \(C\left(9,3\right)\)thỏa mãn nên nó thuộc đồ thị của hàm số đã cho, các điểm khác không thuộc.

1, \(x=13-4\sqrt{10}=\frac{26-8\sqrt{10}}{2}=\frac{10-2.4.\sqrt{10}+16}{2}=\frac{\left(\sqrt{10}-4\right)^2}{2}\)
Ta có: \(Q=x+\sqrt{5x}-2\sqrt{2x}-2\sqrt{10}\)
\(=\sqrt{x}\left(\sqrt{x}+\sqrt{5}\right)-2\sqrt{2}\left(\sqrt{x}+\sqrt{5}\right)\)
\(=\left(\sqrt{x}+\sqrt{5}\right)\left(\sqrt{x}-2\sqrt{2}\right)\)
\(=\left(\frac{4-\sqrt{10}}{\sqrt{2}}+\sqrt{5}\right)\left(\frac{4-\sqrt{10}}{\sqrt{2}}-2\sqrt{2}\right)\)
\(=\left(2\sqrt{2}-\sqrt{5}+\sqrt{5}\right)\left(2\sqrt{2}-\sqrt{5}-2\sqrt{2}\right)\)
\(=2\sqrt{2}.\left(-\sqrt{5}\right)=-2\sqrt{10}\)
2, a, Để đồ thị h/s đi qua gốc tọa độ thì x=y=0
Ta có: \(-2m-1=0\Leftrightarrow m=\frac{-1}{2}\)
b, giao điểm của h/s y=x-2m-1 với trục hoành A(2m+1;0) với trục tung B(0;-2m-1)
Có: OA=2m+1; OB=|-2m-1|=2m+1
Áp dụng hệ thức lượng trong tam giác vuông coS:
\(\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}=\frac{1}{\left(2m+1\right)^2}+\frac{1}{\left(2m+1\right)^2}=\frac{2}{\left(2m+1\right)^2}\)
\(\Leftrightarrow\frac{\left(2m+1\right)^2}{2}=\left(\frac{\sqrt{2}}{2}\right)^2=\frac{1}{2}\)
\(\Leftrightarrow\left(2m+1\right)^2=1\Leftrightarrow\orbr{\begin{cases}2m+1=1\\2m+1=-1\end{cases}\Leftrightarrow\orbr{\begin{cases}m=0\\m=-1\end{cases}}}\)
c, Hoành độ trung điểm I của AB là: \(x_I=\frac{x_A+x_B}{2}=\frac{2m+1}{2}\)
Tung độ trung điểm I của AB: \(y_I=\frac{y_A+y_B}{2}=\frac{-\left(2m+1\right)}{2}\)
Ta có: \(y_I=-x_I\)=> quỹ tích trung điểm I của AB là đường thẳng y=-x

Xét pt tọa độ giao điểm:
X²=(m+4)x-2m-5
<=> -x²+(m+4)x-2m-5
a=-1. b= m+4. c=2m-5
Để pt có 2 No pb =>∆>0
=> (m+4)²-4×(-1)×2m-5>0
=> m² +2×m×4+16 +8m-20>0
=> m²+9m -2>0
=> x<-9 và x>0
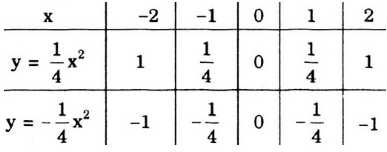
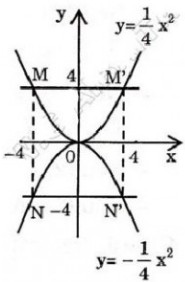

Lần lượt thay tọa độ các điểm M, O, P, Q, A vào hàm số f ( x ) = - 1 4 x ta được:
+) Với M (0; 4), thay x = 0; y = 4 ta được 4 = - 1 4 .0 ⇔ 4 = 0 (vô lý) nên M ∉ (C)
+) Với O (0; 0), thay x = 0 ; y = 0 ta được 0 = - 1 4 .0 ⇔ 0 = 0 (luôn đúng) nên O ∈ (C)
+) Với P (4; −1), thay x = 4 ; y = − 1 ta được −1 = - 1 4 . 4 ⇔ 1 = −1 (luôn đúng) nên P ∈ (C)
+) Với Q (−4; 1), thay x = − 4 ; y = 1 ta được 1 = - 1 4 .(−4) ⇔ 1 = 1 (luôn đúng) nên Q ∈ (C)
+) Với A (8; −2), thay x = 8 ; y = − 2 ta được −2 = - 1 4 .8 ⇔ −2 = −2 (luôn đúng) nên A ∈
Đáp án cần chọn là: A