Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
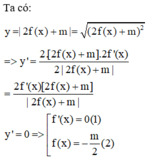
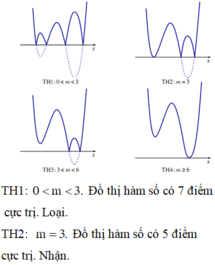
Bài toán cần 5 điểm cực trị => Tổng số nghiệm của (1) và (2) phải là 5
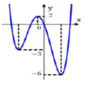
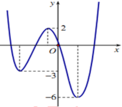
Đối với (1) => số nghiệm chính là số điểm cực trị. Nhìn vào đồ thị => có 3 cực trị
=> Phương trinh (2) phải có 2 nghiệm khác 3 nghiệm trên. Nhìn vào đồ thị ta thấy
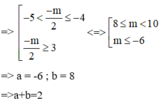

\(\Leftrightarrow\left(a+1,b+2\right)\in\left\{\left(1;3\right);\left(3;1\right);\left(-1;-3\right);\left(-3;-1\right)\right\}\)
\(\Leftrightarrow\left(a,b\right)\in\left\{\left(0;1\right);\left(2;-1\right);\left(-2;-5\right);\left(-4;-3\right)\right\}\)

ta có \(\left|x-a\right|+\left|x-b\right|+\left|x-c\right|+\left|x-d\right|\ge\left|\left(x-a\right)+\left(x-b\right)+\left(c-x\right)+\left(d-x\right)\right|=\left|c+d-a-b\right|=c+d-a-b\)( do a<b<c<d => c-a>0 và d-b>0)
vậy Min A= c+d-a-b

Áp dụng BĐT : \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) ta được:
P=-|3x-18|-|3x+7|=-|18-3x|-|3x+7|=-(|18-3x|+|3x+7|)\(\le\)-25
Dấu "=" xảy ra khi: (18-3x)(3x+7)\(\ge\)0
Giải cái đó ra bạn sẽ được: -7/3 \(\le x\le\)6
Mà x nguyên nên: x={-2;-1;0;1;2;3;4;5;6} có 9 phần tử
Vậy chọn C
Áp dụng \(\left|a\right|-\left|b\right|\le\left|a-b\right|\) (dấu = xảy ra khi a,b > 0), ta có :
\(P=-\left|3x-18\right|-\left|3x+7\right|=-\left|3x-18\right|-\left|7+3x\right|\le-\left|\left(3x-18\right)-\left(7+3x\right)\right|\)
\(=-\left|3x-18-7-3x\right|=-\left|-18-7\right|=-25\)
GTLN của P là -25 <=> 3x - 18 > 0 và 3x + 7 > 0
<=> 3x > 18 và 3x > -7 => x > 6
Vậy có vô số giá trị của x thỏa mãn P có GTLN với điều kiện x > 6 và x là số nguyên

\(M>\frac{x}{x+y+z+t}+\frac{y}{x+y+z+t}+\frac{z}{x+y+z+t}+\frac{t}{x+y+z+t}=\frac{x+y+z+t}{x+y+z+t}=1\)
Mà \(\frac{a}{b}<1\) thì \(\frac{a}{b}<\frac{a+m}{b+m}\) ; \(m\in N\)*
Do đó \(M<\frac{x+t}{x+y+z+t}+\frac{y+z}{x+y+z+t}+\frac{z+x}{x+y+z+t}+\frac{t+y}{x+y+z+t}=\frac{2\left(x+y+z+t\right)}{x+y+z+t}=2\)
Vậy 1 < M < 2 nên M không phải là số tự nhiên/

Ta có :
\(\frac{\left|2x-3\right|+2^{2015}}{\left|3-2x\right|+3^{2015}}=\frac{\left|2x-3\right|+2^{2015}}{\left|2x-3\right|+3^{2015}}\) có GTNN
\(\Leftrightarrow\left|2x-3\right|\) có GTNN
\(\Leftrightarrow\left|2x-3\right|=0\)
\(\Leftrightarrow2x=3\)
\(\Leftrightarrow x=1,5\)
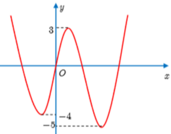
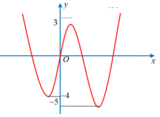




Đáp án là A