Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
? Lời giải:
+ Với giải thiết bài toán x 1 v 2 + x 2 v 1 = 8 c m 2 / s
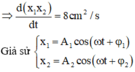
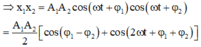
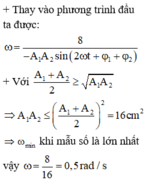

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)

T=2pi/4pi=0.5(s) => f=2 sau 5 s nó trở lại trạng thái ban đầu x=4cos(0)=4 vật ở biên
T=1(s)tại t=T/6 . ban đầu t=0 vật ở vtcb sau T/6 vật ở vị trí x=(a căn 3)/2 vì cos dương => -sin <0 => vật đi theo chiều âm . áp dụng ptđộc lâp tg cho v và a tìm nốt dc a

Áp dụng công thức độc lập, ta có: \(A^2 = x^2+\frac{v^2}{\omega^2} \Rightarrow\) \(8^2+\frac{12^2}{\omega^2} = 6^2+\frac{16^2}{\omega^2} \Rightarrow \omega = 2 \ (rad/s) \Rightarrow f = \frac{1}{\pi} \ Hz\)

Combo 3 câu :)
4/ \(f=5Hz\Rightarrow\omega=10\pi\left(rad/s\right)\)
\(A^2=x^2+\frac{v^2}{\omega^2}\Leftrightarrow A=\sqrt{\left(2\sqrt{3}\right)^2+\frac{20^2\pi^2}{10^2\pi^2}}=4\left(cm\right)\)
\(2\sqrt{3}=4\cos\varphi\Rightarrow\varphi=\pm\frac{\pi}{6}\)
\(v=-20\pi< 0\Rightarrow\varphi>0\Rightarrow\varphi=\frac{\pi}{6}\)
\(\Rightarrow x=4\cos\left(10\pi t+\frac{\pi}{6}\right)\)
5/ \(A^2=\frac{a^2}{\omega^4}+\frac{v^2}{\omega^2}\Rightarrow A=\sqrt{\frac{a^2}{\omega^4}+\frac{v^2}{\omega^2}}=...\)
6/ Áp dụng công thức ở câu 5
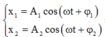
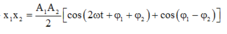
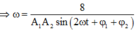

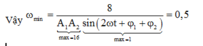
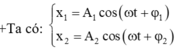
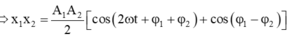
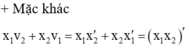
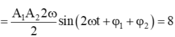
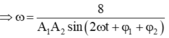
 chọn A
chọn A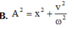
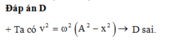
Chọn đáp án B
? Lời giải:
+ Với giải thiết bài toán x 1 v 1 + x 2 v 2 = 8 c m 2 / s ⇒ d x 1 x 2 d t = 8 c m 2 / s
Giả sử x 1 = A 1 cos ω t + φ 1 x 2 = A 2 cos ω t + φ 2
⇒ x 1 x 2 = A 1 A 2 cos ω t + φ 1 cos ω t + φ 2 = A 1 A 2 2 cos φ 1 − φ 2 + cos 2 ω t + φ 1 + φ 2
+ Thay vào phương trình đầu ta được ω = 8 − A 1 A 2 sin 2 ω t + φ 1 + φ 2
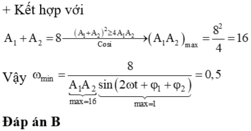
+ Với A 1 + A 2 2 ≥ A 1 A 2 ⇒ A 1 A 2 ≤ A 1 + A 2 2 2 = 16 c m 2
⇒ ω min khi mẫu số là lớn nhất vậy ω = 8 16 = 0 , 5 r a d / s