Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

7/ Em sửa lại đề ạ
Cho hai số thực dương a, b thỏa mãn a+b=4ab
Chứng minh rằng \(\frac{a}{4b^2+1}+\frac{b}{4a^2+1}\ge\frac{1}{2}\)
Đổi biến \(\left(a,b\right)\rightarrow\left(\frac{1}{x},\frac{1}{y}\right)\)
Từ giả thiết => x+y=4
Ta có: BĐT cần CM tương đương với:
\(\frac{\frac{1}{x}}{\frac{4}{y^2}+1}+\frac{\frac{1}{y}}{\frac{4}{x^2}+1}\ge\frac{1}{2}\)\(\Leftrightarrow\frac{y^2}{x\left(4+y^2\right)}+\frac{x^2}{y\left(4+x^2\right)}\ge\frac{1}{2}\left(1\right)\)
Áp dụng BĐT Schwarz, ta có:
∑\(\frac{x^2}{y\left(4+x^2\right)}\ge\frac{\left(x+y\right)^2}{4\left(x+y\right)+xy^2+x^2y}=\frac{16}{16+xy^2+x^2y}\)
Ta chỉ cần chứng minh:
\(xy^2+x^2y\le16\Leftrightarrow xy^2+x^2y\le\frac{1}{4}\left(x+y\right)^3\)
\(\Leftrightarrow xy^2+x^2y\le x^3+y^3\)(luôn đúng)
Do đó (1) đúng. BĐT được chứng minh. Dấu "=" xảy ra khi x=y=2⇔a=b=\(\frac{1}{2}\)
6. (chuyên Hòa Bình)
Cho các số dương x, y, z thỏa mãn: xy+zx+4yz=32
Tìm giá trị nhỏ nhất của\(P=x^2+16y^2+16z^2\)
Áp dụng bất đẳng thức Cauchy cho ba số dương x,y,z ta có
\(\hept{\begin{cases}8y^2+\frac{1}{2}x^2\ge2\sqrt{8y^2.\frac{1}{2}x^2}=4xy\\8z^2+\frac{1}{2}x^2\ge2\sqrt{8z^2.\frac{1}{2}x^2}=4xz\\8y^2+8z^2\ge2\sqrt{8y^2.8z^2}=16yz\end{cases}}\)
Cộng từng vế của ba bđt trên ta có
\(P\ge4\left(xy+xz+4yz\right)=4.32=128\)

Đáp án C
Ta có x + y = 3 ⇒ y = 3 − x ≥ 1 ⇔ x ≤ 2 ⇒ x ∈ 0 ; 2
Khi đó P = f x = x 3 + 2 3 − x 2 + 3 x 2 + 4 x 3 − x − 5 x = x 3 + x 2 − 5 x + 18
Xét hàm số f x = x 3 + x 2 − 5 x + 18 trên đoạn 0 ; 2 , có f ' x = 3 x 2 + 2 x − 5
Phương trình 0 ≤ x ≤ 2 3 x 2 + 2 x − 5 = 0 ⇔ x = 1. Tính f 0 = 18 , f 1 = 15 , f 2 = 20
Vậy min 0 ; 2 f x = 15 , m a x 0 ; 2 f x = 20 hay P m a x = 20 và P min = 15

Đáp án C
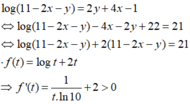
Suy ra f(t) đồng biến trên TXĐ và pt f(t) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 − 2 x − y = 10 ⇒ y = 1 − 2 x ⇒ P = 16 x 2 ( 1 − 2 x ) − 2 x ( 3 − 6 x + 2 ) − 1 + 2 x + 5 = − 32 x 3 + 28 x 2 − 8 x + 4 P ' = − 96 x 2 + 56 x − 8 P ' = 0 ⇔ x = 1 4 x = 1 3 P ( 0 ) = 4 , P ( 1 3 ) = 88 27 , P ( 1 4 ) = 13 4 , P ( 1 2 ) = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

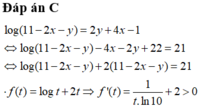
Suy ra f(t) đồng biến trên TXĐ và pt f ( t ) = 21 chỉ có 1 nghiệm duy nhất
Ta thấy t = 10 là 1 nghiệm của pt nên t = 10 là nghiệm duy nhất của pt
⇒ 11 - 2 x - y = 10 ⇒ y = 1 - 2 x ⇒ P = 16 x 2 1 - 2 x - 2 x 3 - 6 x + 2 - 1 + 2 x + 5 = - 32 x 3 + 28 x 2 - 8 x + 4 P ' = - 96 x 2 + 56 x - 8 P ' = 0 ⇔ [ x = 1 4 x = 1 3 P 0 = 4 , P 1 3 = 88 27 , P 1 4 = 13 4 , P 1 2 = 3 ⇒ m = 13 4 , M = 4 ⇒ M + 4 m = 17

Ta có :
\(\frac{\left|2x-3\right|+2^{2015}}{\left|3-2x\right|+3^{2015}}=\frac{\left|2x-3\right|+2^{2015}}{\left|2x-3\right|+3^{2015}}\) có GTNN
\(\Leftrightarrow\left|2x-3\right|\) có GTNN
\(\Leftrightarrow\left|2x-3\right|=0\)
\(\Leftrightarrow2x=3\)
\(\Leftrightarrow x=1,5\)

\(P=xy\left(x-2\right)\left(y+6\right)+13x^2+4y^2-26x+24y+46.\)
\(=\left(x^2-2x\right)\left(y^2+6y\right)+13\left(x^2-2x\right)+4\left(y^2+6y\right)+46\)
\(=\left[\left(x^2-2x\right)\left(y^2+6y\right)+4\left(y^2+6y\right)\right]+13\left(x^2-2x+4\right)-6\)
\(=\left(x^2-2x+4\right)\left(y^2+6y\right)+13\left(x^2-2x+4\right)-6\)
\(=\left(x^2-2x+4\right)\left(y^2+6y+13\right)-6\)
\(=\left[\left(x-1\right)^2+3\right]\left[\left(y+3\right)^2+4\right]-6\)
Ta có \(\left(x-1\right)^2\ge0\forall x\Rightarrow\left(x-1\right)^2+3\ge3\)
\(\left(y+3\right)^2\ge0\forall y\Rightarrow\left(y+3\right)^2+4\ge4\)
Suy ra \(P=\left[\left(x-1\right)^2+3\right]\left[\left(y+3\right)^2+4\right]-6\ge3.4-6=6\)
Vậy giá trị nhỏ nhất của P=6 \(\Leftrightarrow\hept{\begin{cases}\left(x-1\right)^2=0\\\left(y+3\right)^2=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=1\\y=-3\end{cases}.}\)
Câu này tương tự với câu có link bên dưới phải không ạ?
https://olm.vn/hoi-dap/detail/223114327893.html
Ta có:
\(P=xy\left(x-2\right)\left(y+6\right)+13x^2+4y^2-26x+24y+46\)
\(=\left[x\left(x-2\right)\right]\left[y\left(y+6\right)\right]+\left(13x^2-26x\right)+\left(4y^2+24y\right)+46\)
\(=\left(x^2-2x\right)\left(y^2+6y\right)+13\left(x^2-2x\right)+4\left(y^2+6y\right)+46\)
\(=\left[\left(x-1\right)^2-1\right]\left[\left(y+3\right)^2-9\right]+13\left[\left(x-1\right)^2-1\right]\)
\(+4\left[\left(y+3\right)^2-9\right]+46\)
Đặt \(x-1=u;y+3=v\)
Khi đó \(P=\left(u^2-1\right)\left(v^2-9\right)+13\left(u^2-1\right)+4\left(v^2-9\right)+46\)
\(=u^2v^2-v^2-9u^2+9+13u^2-13+4v^2-36+46\)
\(=u^2v^2+4u^2+3v^2+6\ge6\)
Đẳng thức xảy ra khi \(\hept{\begin{cases}u=0\\v=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x-1=0\\y+3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=-3\end{cases}}\)

Đáp án C