Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
Thực hiện phép tính và điền vào chỗ trống ta được bảng sau:
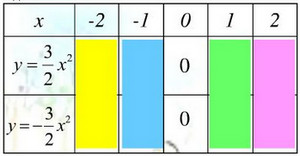
Vẽ đồ thị:
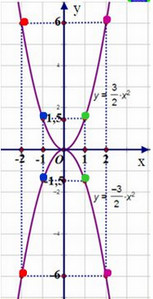
Nhận xét: Đồ thị của hai hàm số đối xứng với nhau qua trục Ox.
Xem thêm tại: http://loigiaihay.com/bai-4-trang-36-sgk-toan-9-tap-2-c44a5695.html#ixzz4dH45gBuO

a) Hpt có nghiệm duy nhất khi \(m\ne3;m\ne4\)
Hpt có vô số nghiệm khi \(\hept{\begin{cases}m=3\\m=4\end{cases}}\)(vô lí). Vậy hệ không thể có vô số nghiệm
b) \(\hept{\begin{cases}3x+my=4\\x+y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}3\left(1-y\right)+my=4\\x=1-y\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(m-3\right)y=1\\x=1-y\end{cases}}\)
\(\cdot m=3\Rightarrow\hept{\begin{cases}0=1\\x=1-y\end{cases}}\)(vô lí)
\(\cdot m>3\Rightarrow\hept{\begin{cases}y=\frac{1}{m-3}>0\\x=1-\frac{1}{m-3}=\frac{m-4}{m-3}\end{cases}}\)
Để \(x< 0\)thì \(\frac{m-4}{m-3}< 0\). Mà \(m-3>0\Leftrightarrow m>3\)nên \(m-4< 0\Leftrightarrow m< 4\)
\(\Rightarrow3< m< 4\)
\(\cdot m< 3\Rightarrow\hept{\begin{cases}y=\frac{1}{m-3}< 0\\x=1-\frac{1}{m-3}=\frac{m-4}{m-3}\end{cases}}\)(loại do \(y< 0\))
Vậy \(3< m< 4\)thì thỏa ycbt

Áp dụng BĐT Cô-si dạng Engel,ta có :
\(\frac{x^2}{x+\sqrt{yz}}+\frac{y^2}{y+\sqrt{xz}}+\frac{z^2}{z+\sqrt{xy}}\ge\frac{\left(x+y+z\right)^2}{x+y+z+\sqrt{xy}+\sqrt{yz}+\sqrt{xz}}\)
Mà \(\sqrt{xy}+\sqrt{yz}+\sqrt{xz}\le x+y+z\)
\(\Rightarrow\)\(\frac{\left(x+y+z\right)^2}{x+y+z+\sqrt{xy}+\sqrt{yz}+\sqrt{xz}}\ge\frac{\left(x+y+z\right)^2}{2\left(x+y+z\right)}=\frac{x+y+z}{2}\ge\frac{3}{2}\)
Dấu "=" xảy ra khi x = y = z = \(\frac{3}{2}\)

\(\sqrt{4x^2-4x+1}=\sqrt{x^2+10x+25}\left(x\ge\frac{1}{2}\right)\)
\(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=\sqrt{\left(x+5\right)^2}\)
\(\Leftrightarrow2x-1=x+5\)
\(\Leftrightarrow2x-1-x-5=0\)
\(\Leftrightarrow x-6=0\Leftrightarrow x=6\left(tm\right)\)
vậy x=6 là nghiệm của phương trình
b) \(\sqrt{x+3}+2\sqrt{4x+12}-\frac{1}{3}\sqrt{9x+27}=8\left(x\ge-3\right)\)
\(\Leftrightarrow\sqrt{x+3}+2\sqrt{4\left(x+3\right)}-\frac{1}{3}\sqrt{9\left(x+3\right)}=8\)
\(\Leftrightarrow\sqrt{x+3}+4\sqrt{x+3}-\sqrt{x+3}=8\)
\(\Leftrightarrow4\sqrt{x+3}=8\)
\(\Leftrightarrow x+3=4\)
<=> x=-1 (tmđk)
vậy x=-1 là nghiệm của phương trình

Mình gợi ý để bạn được người khác giúp nhé. Khi đăng bài bạn nên đăng từng câu. Đừng đăng nhiều câu cùng lúc vì nhìn vô không ai muốn giải hết. Giờ bạn tách ra từng câu đăng lại đi. Sẽ có người giúp đấy