Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
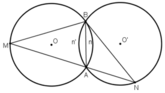
+ (O) và (O’) là hai đường tròn bằng nhau
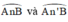cùng được căng bởi dây AB
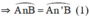
+ (O) có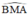 
là góc nội tiếp chắn cung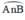 
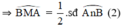
+ (O’) có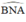 
là góc nội tiếp chắn cung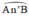 
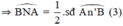
Từ (1); (2); và (3) suy ra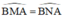 
⇒ ΔBMN cân tại B.
Do hai đường tròn bằng nhau nên hai cung nhỏ AB bằng nhau. Vì cùng căng dây AB.
Suy ra 
= 
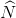(cùng chắn hai cung bằng nhau) nên tam giác BMN là tam giác cân đỉnh B
a: góc BMA=góc CNA=90 độ
=>MB//NC
=>IK//MB//NC
=>IK vuông góc MN
góc AIK+góc AHK=90+90=180 độ
=>AHIK nội tiếp
b: ΔHMN đồng dạng với ΔABC
=>góc MHN=góc BAC cố định
\(S_{HMN}=\dfrac{1}{2}\cdot HM\cdot HN\cdot sin\widehat{MHN}< =\dfrac{1}{2}\cdot AB\cdot AC\cdot sin\widehat{BAC}\)
Dấu = xảy ra khi MH là đừog kính của (O) và NH là đường kính của (O')
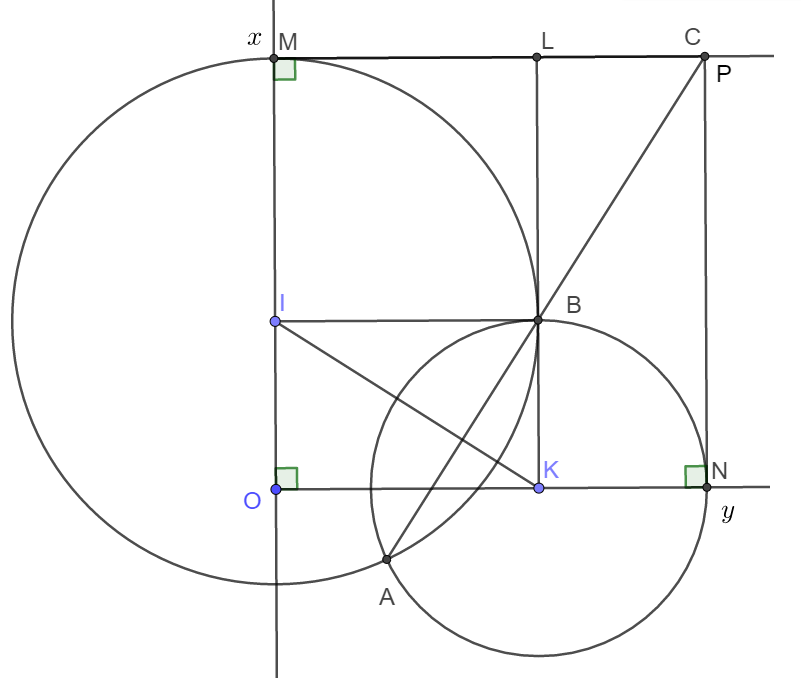
a) Trong tam giác OIK có:
|OK −− OI| < IK < |OK + OI| hay ∣R−r∣<IK<∣R+r∣∣R−r∣<IK<∣R+r∣.
Vậy hai đường tròn (I) và (K) luôn cắt nhau.
b) Dễ thấy tứ giác OMCN là hình chữ nhật (Tứ giác có 3 góc vuông).
Mà OM = OI + IM = OI + OK;
ON = OK + KN = OK + OI.
Vậy OM = ON hay hình chữ nhật OMCN là hình vuông.
c) Gọi giao điểm của BK và MC là L và giao điểm của AB với MC là P.
Tứ giác IBKO là hình chữ nhật. Suy ra IB = OK.
Tứ giác MLBI là hình vuông nên ML = BI, BL = OK.
Từ đó suy ra ΔBLP=ΔKOIΔBLP=ΔKOI. Vì vậy LP = OI.
Suy ra MP = ON = MC. Hay điểm C trùng với P.
Suy ra ba điểm A, B, C thẳng hàng.
d) Nếu OI + OK = a (không đổi) thì OM = MC = a không đổi. Suy ra điểm C cố định.
Vậy đường thẳng AB luôn đi qua điểm C cố định.
Xét tứ giác ACDB có A,C,D,B cùng nằm trên (O)
nên ACDB là tứ giác nội tiếp
=>\(\widehat{CAB}+\widehat{CDB}=180^0\)
mà \(\widehat{CAB}+\widehat{MAC}=180^0\)(hai góc kề bù)
nên \(\widehat{MAC}=\widehat{CDB}=\widehat{MDB}\)
Xét tứ giác AEFB có A,E,F,B cùng nằm trên (O')
nên AEFB là tứ giác nội tiếp
=>\(\widehat{BAE}+\widehat{BFE}=180^0\)
mà \(\widehat{BAE}+\widehat{MAE}=180^0\)(hai góc kề bù)
nên \(\widehat{MAE}=\widehat{MFB}\)
Xét ΔMCA và ΔMBD có
\(\widehat{MAC}=\widehat{MDB}\)
\(\widehat{M}\) chung
Do đó: ΔMCA đồng dạng với ΔMBD
=>\(\dfrac{MC}{MB}=\dfrac{MA}{MD}\)
=>\(MC\cdot MD=MA\cdot MB\)(1)
Xét ΔMAE và ΔMFB có
\(\widehat{MAE}=\widehat{MFB}\)
\(\widehat{M}\) chung
Do đó: ΔMAE đồng dạng với ΔMFB
=>\(\dfrac{MA}{MF}=\dfrac{ME}{MB}\)
=>\(MA\cdot MB=MF\cdot ME\left(2\right)\)
Từ (1) và (2) suy ra \(MC\cdot MD=ME\cdot MF\)
=>\(\dfrac{MC}{MF}=\dfrac{ME}{MD}\)
Xét ΔMCE và ΔMFD có
\(\dfrac{MC}{MF}=\dfrac{ME}{MD}\)
\(\widehat{CME}\) chung
Do đó: ΔMCE đồng dạng với ΔMFD
=>\(\widehat{MCE}=\widehat{MFD}\)
mà \(\widehat{MCE}+\widehat{DCE}=180^0\)(hai góc kề bù)
nên \(\widehat{MFD}+\widehat{DCE}=180^0\)
=>CDFE là tứ giác nội tiếp
+ (O) và (O’) là hai đường tròn bằng nhau
+ (O) có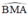
là góc nội tiếp chắn cung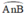 
+ (O’) có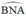
là góc nội tiếp chắn cung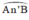 
Từ (1); (2); và (3) suy ra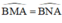
⇒ ΔBMN cân tại B.
Kiến thức áp dụng
+ Trong cùng một đường tròn hoặc hai đường tròn bằng nhau, hai dây bằng nhau căng hai cung bằng nhau.
+ Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.