Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 6 :
Tự vẽ hình nhá :)
a) Gọi O là giao điểm của AC và EF
Xét tam giác ADC có :
EO // DC => AE/AD = AO/AC (1)
Xét tam giác ABC có :
OF // DC
=> CF/CB = CO/CA (2)
Từ (1) và (2) => AE/AD + CF/CB = AO/AC + CO/CA = AO + CO/AC = AC/AC = 1 => đpcm
Bài 7 :
A B C D G K M F E
a) Do EF // AB => CF / CA = EF / AB => CF / EF = AC / AB (1)
Dựng MG // AC và M là trung điểm của cạnh BC => GM là đường trung bình của tam giác ABC => G là trung điểm của cạnh AB =>AG = BG
Do DK // GM => AD / AG = DK / GM => AD / BG = DK / GM
=> DK / AD = GM / BG = \(\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB} \left(2\right)\)
Từ (1) và (2) => CF / EF = DK / AD
Mà tứ giác ADEF là hình bình hành ( vì EF // AD và DE // AF ) nên AD = È
=> CF = DK ( đpcm )
Bài 8 :
A B C M N 38 11 8
Ta có : AB = AM + MB = 11 + 8 = 19 ( cm )
Áp dụng hệ quả định lí Ta-lét vào tam giác ABC, ta có :
AM / AB = AN / AC => AM + AB / AB = AN + AC / AC => 19 + 11 / 19 = AN + 38 / 38 => 30/19 = 38 + AN / 38
=> 1140 = 19.AN + 722
=> AN = ( 1140 - 722 ) / 19 = 22 ( cm )
=> NC = 38 - 12 = 26 ( cm )

Gọi E là trung điểm KL; I là trung điểm AG
\(\left\{{}\begin{matrix}KE=EL\\BD=DC\end{matrix}\right.\Rightarrow ED\) là đtb hthang \(BCLK\left(BK//LC.do.cùng.\perp KL\right)\)
\(\Rightarrow ED=\dfrac{BK+CL}{2}\Rightarrow2ED=BK+CL\left(1\right)\)
Vì G là trọng tâm tam giác ABC nên \(GD=\dfrac{1}{2}AG\)
Mà \(AI=IG=\dfrac{1}{2}AG\) nên \(GD=AI=IG\)
Ta có \(ED//BK//LC\left(t/c.đtb\right)\Rightarrow ED\perp KL\left(BK\perp KL\right)\)
Áp dụng định lí Ta-lét cho \(AH//ED\left(\perp KL\right)\) ta có
\(\dfrac{AH}{ED}=\dfrac{AG}{GD}=2\Rightarrow AH=2ED\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow AH=BK+CL\)

a) △ AKB ~ △AIC (g - g) ( ˆK=ˆI=900;K^=I^=900;ˆAA^ chung) (3)
⇒ ˆACI=ˆABKACI^=ABK^
⇒ 900−ˆACI=900−ˆABK900−ACI^=900−ABK^
⇒ ˆHCD=ˆHBDHCD^=HBD^ (1)
xét tứ giác AKHI có
ˆKHI=3600−ˆA−ˆHKA−ˆHIA=1800−ˆAKHI^=3600−A^−HKA−^HIA^=1800−A^
tương tự ˆD=1800−ˆAD^=1800−A^
⇒ ˆKHI=ˆDKHI^=D^ (2)
từ (1) và (2) ⇒ BHCD là hình bình hành
b) từ (3) ⇒ AIAK=ACABAIAK=ACAB (4)
⇒ AI.AB = AK.AC
c) xét △AKI và △ABC có
ˆAA^ chung; (4)
⇒ △AKI ~ △ABC (c-g-c)
d) gọi K là giao của DH và BC
vì A,D,H thăng hàng và H là trực tâm nên AD ⊥ BC hay HD ⊥ BC
⇒ BDCH là hình thoi
⇒ KC = KB
⇒ △ ABK = △ ACK (c-g-c)
⇒ △ ABC cân tại A
vậy △ ABC cân tại A thì DH đi qua A và BHCD là hình thoi
nó bị lỗi mk gửi lại
a) △ AKB ~ △AIC (g - g) ( ˆK=ˆI=900,ˆAA^ chung) (3)
⇒ ˆACI=ˆABK
⇒ 900−ˆACI=900−ˆABK
⇒ ˆHCD=ˆHBD (1)
xét tứ giác AKHI có
ˆKHI=3600−ˆA−ˆHKA−ˆHIA=1800−ˆA
tương tự ˆD=1800−ˆAD^=1800−A^
⇒ ˆKHI=ˆD (2)
từ (1) và (2) ⇒ BHCD là hình bình hành
b) từ (3) ⇒ AI/AK=AC/AB (4)
⇒ AI.AB = AK.AC
c) xét △AKI và △ABC có
ˆAA^ chung; (4)
⇒ △AKI ~ △ABC (c-g-c)
d) gọi K là giao của DH và BC
vì A,D,H thăng hàng và H là trực tâm nên AD ⊥ BC hay HD ⊥ BC
⇒ BDCH là hình thoi
⇒ KC = KB
⇒ △ ABK = △ ACK (c-g-c)
⇒ △ ABC cân tại A
vậy △ ABC cân tại A thì DH đi qua A và BHCD là hình thoi
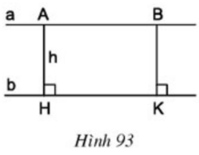


AH // BK (cùng ⊥ b) và AB // HK ⇒ tứ giác ABKH là hình bình hành
⇒ AH = BK = h