Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
- Tại thời điểm t = 0 hai điểm sáng cùng đi qua VTCB theo chiều dương
+ Phương trình dao động của hai điểm sáng:

+ Ở VTCB theo chiều dương hai điểm sáng có cùng độ lớn vật tốc

- Công thức tính vận tốc tại thời điểm t: ![]()
Khi vận tốc của điểm sáng 1 bằng 0 thì vận tốc của điểm sáng 2 mới giảm lần:
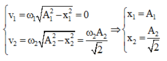
Biểu diễn trên đường tròn lượng giác ta có:
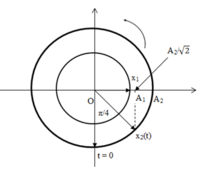
Từ đường tròn lượng giác ta thấy: cùng trong khoảng thời gian t, góc quét được của hai chất điểm lần lượt là:
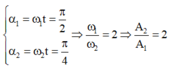
- Thời điểm hai điểm sáng có cùng vận tốc:
![]()
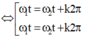
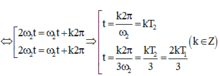
Với k = 0 => thời điểm đầu tiên hai điểm sáng có cùng độ lớn vận tốc.
Với k = 1 => thời điểm tiếp theo hai điểm sáng có cùng độ lớn vận tốc là: ![]()
=> Góc quét được tương ứng của hai chất điểm trên đường tròn:

Biểu diễn trên đường tròn lượng giác:
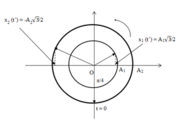
Từ đường tròn lượng giác ta có tỉ số độ lớn li độ của hai điểm sáng:
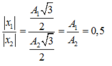

\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

\(v=126\cos(5\pi t+\dfrac{\pi}{3})\)
Giá trị vận tốc này sẽ không cho kết quả đẹp, bạn kiểm tra lại xem biểu thức vận tốc đúng chưa nhé.

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

Đáp án A
Tại  →
→
Chất điểm A có li độ ![]() ;
;
Áp dụng công thức:
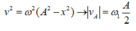
Tại 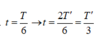 ,
,
với T’ là chu kì của B → B cũng có li độ ![]()
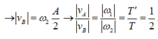
Đáp án C