Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
lim x → 0 f x = lim x → 0 x + 4 − 4 − x x = lim x → 0 x + 4 − 4 + x x x + 4 − 4 − x = lim x → 0 2 x + 4 − 4 − x = 1 2
Để hàm số f(x) liên tục tại x=0 thì f 0 = 1 2

\(\lim\limits_{x\rightarrow0}\left|f\left(x\right)\right|=\lim\limits_{x\rightarrow0}\left|x^2sin\dfrac{1}{x}\right|< \lim\limits_{x\rightarrow0}\left|x^2\right|=0\).
Vậy \(\lim\limits_{x\rightarrow0}f\left(x\right)=0\).
\(f\left(0\right)=A\).
Để hàm số liên tục tại \(x=0\) thì \(\lim\limits_{x\rightarrow0}f\left(x\right)=f\left(0\right)\Leftrightarrow A=0\).
Để xét hàm số có đạo hàm tại \(x=0\) ta xét giới hạn:
\(\lim\limits_{x\rightarrow0}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0}\dfrac{x^2sin\dfrac{1}{x}}{x}=\lim\limits_{x\rightarrow0}xsin\dfrac{1}{x}=0\).
Vậy hàm số có đạo hàm tại \(x=0\).

Đáp án C
lim x → 0 f ( x ) = lim x → 0 x + 2 - 2 - x x = lim x → 0 x + 2 - 2 + x x x + 2 + 2 - x = lim x → 0 2 x + 2 + 2 - x = 1 2
Vậy hàm số liên tục tại x=0 khi và chỉ khi f(0)= lim x → 0 f ( x ) = 1 2
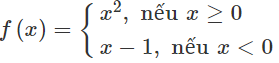

Chọn A