Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng thời gian giữa hai lần liên tiếp cường độ dòng điện bằng 0 là ∆t = T/2 = 1/2f = 1/80s.
Chọn đáp án B

Giải thích: Đáp án C
Khoảng thời gian giữa haii lần liên tiếp để cường độ bằng không là T/2.
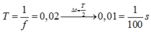

T=0.1
t2=t1+0.025=t1+T/4-->\(x_1^2+x_2^2=A^2\)-->x22=12
ma tai t1 dong giam va t2=t1+T/4 --->X2=-2\(\sqrt{3}\)

Sử dụng đường tròn
Từ thời điểm 0-0.01 s thì góc quay được là \(\varphi = 0.01.\omega = \pi (rad).\)
I 0 π/3 t=0 M N I 0 2 I 0 2 - t=0.01 P Q t 1 t 2 π/6 φ1 φ2
Thời điểm t =0 ứng với điểm M; thời điểm t = 0.01s ứng với điểm N. Từ M đến N sẽ qua hai điểm P và Q có giá trị (độ lớn) 0.5I0.
tại P: \(\varphi_1 = t_1 \omega => t_1 = \frac{\pi/3}{100\pi} = \frac{1}{300}s\)
tại Q: \(\varphi_2 = t_2 \omega => t_2 = \frac{\pi/3+\pi/6+\pi/6}{100\pi} = \frac{2}{300}s\)
chọn đáp án. A

Ban đầu (t=0) dòng điện có giá trị cực đại. Để dòng điện giảm về 0 thì mất thời gian T/4
Suy ra T/4 = 0,004
⇒ T = 0,016s
Tần số f = 1/T = 62,5Hz


Bạn cần tìm vị trí li độ ứng với t = 1/200 thì thay vào hàm i => i =2(VTBiên dương) ở vị trí B như hình vẽ.
Tương tự thay t = 0.015 vào i => i = -2 (VTBiên âm).C
Có 1 vị trí có giá trị \(A\sqrt{2}\) như hình vẽ
Tìm góc quay được \(\cos\varphi_1=\frac{A\sqrt{2}}{A}=\sqrt{2}\Rightarrow\varphi_1=\frac{\pi}{4}.\)
=> Thời gian quay ứng với góc phi 1 là \(t=\frac{\varphi_1}{\omega}=0.0025s.\)
Như vậy thời điểm vật ở li độ \(A\sqrt{2}\) là \(t_M=t_1+t=\frac{1}{200}+0.0025=0.0075s.\)
Đáp án B
+ Khoảng thời gian giữa hai lần liên tiếp cường độ dòng điện bằng 0 là
∆ t = T 2 = 1 2 f = 1 2 . 40 = 1 80 s