Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ∆BCA = ∆ MND; ∆ ABC = ∆DNM; ∆ BAC = ∆ MDN;…
b) Vì ∆ABC = ∆ DMN nên AB = DM; AC = DN; BC = MN
Mà AB = 3cm, AC = 4cm, MN = 6cm
Suy ra: DM = 3cm, DN = 4cm, BC = 6cm
Chu vi ∆ABC là: AB + AC + BC = 3 + 4 + 6 = 13 (cm)
Chu vi ∆DMN là: DM + DN + MN = 3 + 4 + 6 = 13 (cm)

A)\(\Delta ACB=\Delta DNM\)
b) ta có : AB = DM = 3 cm
AC = DN = 4 cm
BC = MN = 6 cm
chu vi \(\Delta ABC=AB+AC+BC=3+4+6=13\left(cm\right)\)
chu vi \(\Delta DMN=DM+MN+DN=3+4+6=13\left(cm\right)\)

Vì \(\Delta ABC=\Delta DEF\)
nên AB = DE = 4cm;
BC = EF = 6cm;
AC = DF = 5cm
Khi đó: \(P_{\Delta ABC}=P_{\Delta DEF}=4+5+6=15\left(cm\right)\)
Vậy \(P_{\Delta ABC}=P_{\Delta DEF}=15cm.\)

a: ΔABC và ΔEFD
Để ΔABC=ΔEFD theo trường hợp c-g-c thì BC=FD
b: ΔABC=ΔEFD
nên AB=EF=5cm; AC=ED=6cm; BC=FD=6cm
=>\(C_{ABC}=C_{EFD}=5+6+6=17\left(cm\right)\)

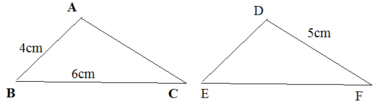
Vì ΔABC = ΔDEF nên suy ra:
AB = DE = 4cm
BC = EF = 6cm
DF = AC = 5cm
Chu vi tam giác ABC bằng:
AB + BC + CA = 4 + 6 + 5 = 15 (cm)
Chu vi tam giác DEF bằng:
DE + EF + DF = 4 + 6 + 5 = 15 (cm)

Ta có:tam giác ABC = tam giác DEF (gt)
\(\Rightarrow\)AB = DE
AC = DF
BC = EF
Mà theo đề ta có : AB = 3cm \(\rightarrow\) DE =3cm ; AC = 4cm \(\rightarrow\)DF =4cm ; EF = 6cm\(\rightarrow\)BC = 6cm
nên ta có chu vi của tam giác ABC là:
AB + AC + BC = 3 + 4 + 6 = 13 (cm)
Vì tam giác ABC = tam giác DEF
Do đó: tam giác DEF có chu vi là : 13 (cm)


Vì ΔABC=ΔDMN nên AB = DM; AC = DN; BC = MN
Mà AB= 3cm, AC = 4cm, MN = 6cm
Suy ra: DM =3cm; DN = 4cm; BC = 6cm
Chu vi ΔABClà: AB+AC+BC = 3+4+6 = 13 cm
Chu vi ΔDMNlà: DM+DN+MN = 3+4+6 = 13 cm