Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Tìm công thức tính số đường chéo: Số đoạn thẳng tạo bởi n đỉnh là C n 2 , trong đó có n cạnh, suy ra số đường chéo là C n 2 - n
+ Đa giác đã cho có 135 đường chéo nên C n 2 − n = 135
+ Giải phương trình
n ! n − 2 ! 2 ! = 135 , n ∈ ℕ , n ≥ 2 ⇔ n − 1 n − 2 n = 270 ⇔ n 2 − 3 n − 270 = 0 ⇔ n = 18 n h a n n = − 15 l o a i ⇔ n = 18

Chọn C
Với hai đỉnh sẽ cho ta một đoạn thẳng, do đó số đoạn thẳng được tạo ra từ n đỉnh là C n 2
Đa giác có n đỉnh sẽ có n cạnh. Trong số C n 2 đoạn thẳng có n đoạn thẳng là cạnh của đa giác. Do đó số đường chéo của đa giác là
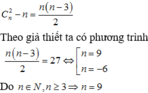

vì 3n^2 chia hết cho 3 nên để A chia hết cho 3 thì ta CM
n^3+2n=n*(n*n+2) vì n là số nguyên nên n có dạng 3k; 3k+1;3k+2(k thuộc Z)
nếu n=3k thì n*(n*n+2) luôn luôn chia hết cho 3
nếu n=3k+1 thì n*n=(3k+1)*(3k+1)=9k^2+3k+3k+1 chia 3 dư 1 nên n*n+2 luôn luôn chia hết cho 3
nếu n=3k+2 thì n*n=(3k+2)*(3k+2)=9k^2+6k+6k+4 chia 3 dư 1 nên n*n+2 luôn luôn chia hết cho 3
vậy biểu thức trên luôn luôn chia hết cho 3 với mọi n thuộcZ
câu b)để A chia hết cho 15 thì n^3+3n^2+2n phải chia hết cho 3;5(vì ƯCLN(3;5)=1)
Mà theo câu a thì A luôn luôn chia hết cho 3 với n thuộc Z
nên ta chỉ cần tìm giá trị của n để A chia hết cho5
để A chia hết cho 5 thì n^3 phải chia hết cho 5;3n^2 phải chia hết cho 5;2n phải chia hết cho 5
nên n phải chia hết cho 5(vì ƯCLN(3;5)=1;ƯCLN(2;5)=1 nên n^3;n^2;n phải chia hết cho 5 nên ta suy ra n phải chia hết cho 5)
mà 1<n<10 nên n=5(n là số nguyên dương)
vậy giá trị của n thỏa mãn đề bài là 5

Lấy 3 còn lại 9 => nó là tg đều khi 2 đỉnh của tg phải cách nhau qua 3 đỉnh khác
Chia đỉnh đa giác thành 3 nhóm, mỗi nhóm có 4 đỉnh kề nhau, khi lấy 1 đỉnh ở nhóm này làm 1 đỉnh tg thì 2 đỉnh kia sẽ nằm tg ứng trong 2 nhóm còn lại, và số cách lấy 1 đỉnh trong 1 nhóm để làm đỉnh đa giác là 4 => có 4 tg đều có thể lập đc
=> Xác suất = ......
Nếu đã hiểu bài này, b có thể đưa ra 1 công thức: đó là nếu đa giác đều có 3n đỉnh (n thuộc N) thì số tam giác đều như trên là n
Chú ý chỉ là quan tâm đến chữ "đều" mà thôi, từ đó suy ra đc những tính chất mà đề yêu cầu, VD trong bài này, tính chất là mỗi đỉnh của tg đều pải cách nhau qua 3 đỉnh khác của đa giác, từ đó mới suy ra cách chọn ntn.
Còn công thức b co thể xem trên GL về tổ hợp xác suất trong hình học.

a)Ta xét trong tam giác ABH có Góc H =90độ
=>BAHˆ+ABHˆ=90
mà BAHˆ+HACˆ=90=A^(gt)
=>ABHˆ=HACˆ
Xét tam giác BHA và Tam giác AIC có:
AB=AC(gt)
H^=AICˆ=90(gt)
ABHˆ=HACˆ(c/m trên)
=>Tam giác BHA=Tam giác AIC(cạnh huyền-góc nhọn)
=>BH=AI(hai cạnh tương ứng)
b)Vì Tam giác BHA=Tam giác AIC(c/m trên)
=>IC=AH(hai cạnh tương ứng)
Xét trong tam giác vuông ABH có:
BH2+AH2=AB2
mà IC=AH
=>BH2+IC2=AB2(th này là D nằm giữa B và M)
Ta có thể c/m tiếp rằng D nằm giữa M và C thì ta vẫn c/m được Tam giác BHA=Tam giác AIC(cạnh huyền-góc nhọn) và BH2+IC2=AC2=AB2
=>BH2+CI2 có giá trị ko đổi
c)Ta xét trong tam giác DAC có IC,AM là 2 đường cao và cắt nhau tại N(AM cũng là đường cao do là trung tuyến của tam giác cân xuất phát từ đỉnh và cũng chính là đường cao của đỉnh đó xuống cạnh đáy=>AM vuông góc với DC)
=>DN chính là đường cao còn lại=>DN vuông góc với AC(là cạnh đối diện đỉnh đó)
d)Ta dễ dàng tính được Tam giác DMN cân tại M=>DM=MN(dựa vào số đo của các góc và 1 số c/m trên)
Từ M kẻ đường thẳng ME vuông góc với AD còn MF vuông góc với IC,Ta dễ dàng c/m được tam giác MED=Tam giác MFN(cạnh huyền-góc nhọn)
=>ME=MF(là hai đường vuông góc tại điểm M gióng xuống hai cạnh của góc HICˆ)
Theo tính chất của đường phân giác(Điểm nằm trên đường phân giác của góc này thì cách đều hai cạnh tạo thành góc đó)=>IM là tia phân giác của HICˆ

n6 - n4 + 2n3 + 2n2
= n2 . (n4 - n2 + 2n +2)
= n2 . [n2(n - 1)(n + 1) + 2(n + 1)]
= n2 . [(n + 1)(n3 - n2 + 2)]
= n2 . (n + 1) . [(n3 + 1) - (n2 - 1)]
= n2. (n + 1)2 . (n2 - 2n + 2)
Với n ∈ N, n > 1 thì n2 - 2n + 2 = (n - 1)2 + 1 > (n - 1)2
Và n2 - 2n + 2 = n2 - 2(n - 1) < n2
Vậy (n - 1)2 < n2 - 2n + 2 < n2
=> n2 - 2n + 2 không phải là một số chính phương.
Chọn C.
Phương pháp:
Số đường chéo của đa giác có n đỉnh