Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

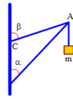
a) T T P O x
P=m.g=5N
b)
P=2.\(cos60^0.T\)
\(\Rightarrow T=\)5N

Để đoạn dây đồng ab cân bằng ta phải có :
P = F
↔ P = 2 . σ . ab = 2 . 4 .10-2 . 5 .10-2
= 40 . 10-4 N = 4 . 10-3 N
Vậy để đoạn dây ab cân bằng ta phải có trọng lượng P = 4 . 10-3 N.
@phynit
Em trả lời 100% . Không có sự tự hỏi tự trả lời đâu ạ ( Em nói để thầy biết và không nghĩ oan cho em )

O A B C D E
l=40cm=0,4m
gốc thế năng tại vị trí vân bằng
a) cơ năng tại C
\(W_C=W_{đ_C}+W_{t_C}=0+m.g.AE\)
(AE=\(l-OE\))
\(\Leftrightarrow W_C=m.g.\left(l-l.cos60^0\right)=\)2J
cơ năng tại B
\(W_B=W_{t_B}+W_{đ_B}=m.g.\left(l-l.cos30^0\right)+\dfrac{1}{2}.m.v_B^2\)
\(\Leftrightarrow\)\(W_B=\)\(4-2\sqrt{3}+\dfrac{1}{2}.mv_B^2\)
bảo toàn cơ năng
\(W_B=W_C\)
\(\Rightarrow v_B\approx\)1,71m/s
vật quay tròn quanh tâm O
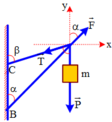
\(\overrightarrow{T}+\overrightarrow{P}=m.\overrightarrow{a_{ht}}\)
chiếu lên trục Ox phương song song dây, chiều dương hướng vào trong
\(T-m.g.cos30^0=m.\dfrac{v_B^2}{l}\)
\(\Rightarrow T\approx16N\)
b) cơ năng tại vị trí cân bằng
\(W_A=0+\dfrac{1}{2}.m.v^2_A\)
bảo toàn cơ năng: \(W_A=W_C\)
\(\Rightarrow v_A=\)2m/s
lực căng dây lúc này
\(T=P+m.\dfrac{v_B^2}{l}\)=20N

a) Bỏ qua lực cản của không khí => Cơ năng được bảo toàn.
Chọn mốc thế năng ở vị trí cân bằng (tại O)
WA= WtA + WđA = WtA (Do vA = 0)
= m.g.hA = 0,2.10. (CO - CH)
= 2.(l-l.cosα) = 2.(1 - 1.cos60o)
= 1 (J)
Khi đó, WO = 1 = WA(J)
<=> WđO = 1 (Do WtO = 0)
<=> \(\dfrac{1}{2}\).m.vO2 = 1
<=> vO = \(\sqrt{10}\)(m/s)
b) Gọi αo là vị trí vật giao động trong đoạn từ 0o đến 60o
Ta có: \(\overrightarrow{F_{hl}}\) = m.\(\overrightarrow{a}\)
<=> \(\overrightarrow{T}+\overrightarrow{P_1}\)= m\(\overrightarrow{a}\)
Chiếu lên chiều dương:
=> T - P1 = m.a (1)
<=> T = m.a + P.cosαo
<=> T = m.a + m.g.cosαo
* Lực căng dây lớn nhất:
Ta gọi D là 1 điểm bất kì trong khoảng từ 0o đến 60o. Ta gọi tại đó vật có góc lệch so với vị trí cân bằng là αo
+) Ta có: hD = l - l.cosαo ( tương tự như hA)
=> WC = WđD + WtD = WA = WtA
<=> \(\dfrac{1}{2}\).m.vD2 + m.g.hD = m.g.hA
<=> \(\dfrac{1}{2}\).m.vD2 + m.g.( l - l.cosαo) = m.g.(l-l.cosα)
Rút vD2 = 2.g.l.(cosαo - cosα)
+) Từ (1) => T - P.cosαo = m.\(\dfrac{v^2}{l}\)
<=> T = m.\(\dfrac{v^2}{l}\) + m.g.cosαo
= m.\(\dfrac{2.g.l.\left(\cos\alpha_o-\cos\alpha\right)}{l}\)+ m.g.cosαo
= m.2.g.(cosαo - cosα) + m.g.cosαo
= m.g.(2cosαo - 2cosα + cosαo)
= m.g.(3cosαo - 2cosα)
Ta có: cosα , m và g không đổi.
=> T max <=> cosα0 lớn nhất
<=> cosαo = 1
<=> αo = 0o
Vậy T max <=> Vật đi qua vị trí cân bằng.
Khi đó:
T max = m.g.(3 - 2cosα)
= 0,2.10.(3-2cos60o) = 4 (N)
60o T O A P h A H C

1.
theo phương pháp tổng hợp hai lực song song cùng chiều
\(F=F_1+F_2=24N\Rightarrow F_2=24-F_1=6N\) và
\(\dfrac{F_1}{F_2}=\dfrac{d_2}{d_1}\)\(\Leftrightarrow\dfrac{18}{6}=\dfrac{d_2}{30-d_2}\Rightarrow d_2=22,5cm\)
2.
. T N P -P
a)
\(sin\alpha=\dfrac{T}{P}\Rightarrow T=m.g.sin\alpha=\)24,5N
b)\(cos\alpha=\dfrac{N}{P}\Rightarrow N=\dfrac{49\sqrt{3}}{2}N\)

Lực tác dụng lên vật m được biểu diễn trên hình vẽ.
Định luật II Niu-tơn cho:
Chọn hệ trục Oxy với chiều dương là chiều chuyển động theo phương Ox, chiếu phương trình (1) lên:
(Ox): Fcosα- fms= ma (2)
(Oy): N + Fsinα – P = 0 (3)
mà fms= μN (4)
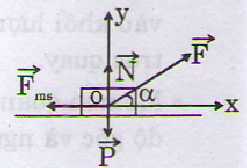
(2), (3) và (4) => F cosα – μ(P- Fsinα ) = ma
=> Fcosα – μP + μFsinα = ma
F(cosα +μsinα) = ma +μmg
=> F =
a) khi a = 1,25 m/s2