Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có :
\(\frac{1}{1^2}< \frac{1}{1.2};\frac{1}{2^2}< \frac{1}{2.3};...;\frac{1}{50^2}< \frac{1}{49.50}\)
\(\Leftrightarrow\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{50^2}< \frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{49.50}=1-\frac{1}{50}< 1< 2\)
Vậy A < 2
\(\frac{1}{1^2}=1\)
\(\frac{1}{2^2}< \frac{1}{1.2}\)
\(\frac{1}{3^2}< \frac{1}{2.3}\)
\(...\)
\(\frac{1}{50^2}< \frac{1}{49.50}\)
\(\Rightarrow\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{50^2}< 1+\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{49.50}\)
\(\Rightarrow A< 1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{49}-\frac{1}{50}\)
\(\Rightarrow A< 1+1-\frac{1}{50}\)
\(\Rightarrow A< 2-\frac{1}{50}< 2\)
Vậy \(A< 2\)

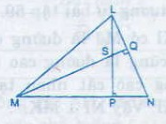
a) Chứng minh NS ⊥ LM
b) Khi =500, hãy tính góc MSP và góc PSQ
Hướng dẫn:
a) Trong ∆NML có :
LP ⊥ MN nên LP là đường cao
MQ ⊥ NL nên MQ là đường cao
mà PL ∩ MQ = {S}
suy ra S là trực tâm của tam giác nên đường thằng SN chứa đường cao từ N hay
SN ⊥ ML
b) ∆NMQ vuông tại Q có =500 nên
=400
∆MPS vuông tại Q có =400 nên
=500
Suy ra =1300(kề bù)


Và đáp án là đây: Nhà của người thợ săn đó ở Cực Bắc.
Các đường kinh tuyến trên Trái đất sẽ tụ về hai điểm Cực Bắc và Cực Nam. Tại điểm Cực Bắc, đi về hướng nào thì cũng sẽ là hướng Nam. Và khi rẽ ngược lên hướng Bắc, người thợ săn đã theo đường kinh tuyến đi về phía điểm Cực bắc - tức là trở về nhà.
giữ lời hứa 1 GP nhé
Nhà của người thợ săn đó ở Cực Bắc.
Các đường kinh tuyến trên Trái đất sẽ tụ về hai điểm Cực Bắc và Cực Nam. Tại điểm Cực Bắc, đi về hướng nào thì cũng sẽ là hướng Nam.
Và khi rẽ ngược lên hướng Bắc, người thợ săn đã theo đường kinh tuyến đi về phía điểm Cực bắc - tức là trở về nhà.

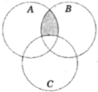
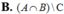
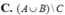
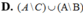


 Mấy pn làm giúp mik câu 2 nha
Mấy pn làm giúp mik câu 2 nha 

Chọn B