Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(I=\lim\limits\dfrac{1+a+a^2+...+a^n}{1+b+b^2+...+b^n}\)
Xet tren tu la 1 csc voi : \(\left\{{}\begin{matrix}u_1=1\\q=a\end{matrix}\right.\Rightarrow S_a=1.\dfrac{a^{n+1}-1}{a-1}\)
Tuong tu cho mau so: \(S_b=1.\dfrac{b^{n+1}-1}{b-1}\)
\(\Rightarrow.....=\lim\limits\dfrac{\dfrac{a^{n+1}-1}{a-1}}{\dfrac{b^{n+1}-1}{b-1}}=\dfrac{\dfrac{1}{a-1}}{\dfrac{1}{b-1}}=\dfrac{1-b}{1-a}\)

\(\lim\limits_{x\rightarrow+\infty}\left(ax-\sqrt{bx^2-2x+2018}\right)=\lim\limits_{x\rightarrow+\infty}x.\lim\limits_{x\rightarrow+\infty}\left(a-\sqrt{b}\right)=\pm\infty\)
Còn tuỳ vào độ lớn của a và b
Đúng là giá trị giới hạn còn phụ thuộc vào giá trị của $a,b$ mới có thể khẳng định nhưng dòng công thức bạn viết ở trên chưa đúng đâu nhé.

1) a) cos7x - √3 sin7x = -√2 (a = 1; b = -√3; c = -√2)
=> a^2 + b^2 =4 > c^2 = 2
Chia 2 vế pt (*) cho \(\sqrt{a^2+b^2}=2\) ta đc:
<=> 1/2cos7x - √3/2 sin7x = -√2/2
<=> sin(π/6)cos7x - cos(π/6)sin7x = sin(-π/4)
<=> sin(π/6 - 7x) = sin(-π/4)
<=> π/6 - 7x = -π/4 + k2π
hoặc (k∈Z)
π/6 - 7x = π + π/4 + k2π
<=> x = 5π/84 + k2π/7
hoặc (k∈Z)
x = -13π/84 + k2π/7
1) b) Ta có:
* 2π/5 < x < 6π/7
<=> 2π/5 < 5π/84 + k2π/7 < 6π/7
<=> 143π/420 < k2π/7 < 67π/84
<=> 143/120 < k < 67/24
=> k ϵ {2}
=> x = 53π/84
* 2π/5 < x < 6π/7
<=> 2π/5 < -13π/84 + k2π/7 < 6π/7
<=> 233/120 < k < 85/24
=> k ϵ {2; 3}
=> x = 5π/12 ; x = 59π/84
Vậy có tất cả 3 nghiệm thỏa mãn (2π/5;6π/7) là x = 53π/84; x = 5π/12 ; x = 59π/84.

Người ta nói tần số của một số A trong một dãy số A1, A2, …,An là số lần xuất hiện của số A trong dãy A1,A2,…,An.
Ví dụ: Cho dãy số 2 3 4 5 1 3 3 4 3
Tần số của số 2 là 1. Tần số của số 3 là 4.
Cho một file văn bản có tên TANSO.INP và có cấu trúc như sau:
Dòng 1: Chứa số nguyên N dương (0<N<=10000)
N dòng tiếp theo: mỗi dòng chứa một số nguyên Ai (0<Ai<101), các số ghi cách nhau ít nhất một dấu cách trống.
Hãy viết chương trình đọc file trên và tìm tần số xuất hiện của các số trong N số đã cho. Yêu cầu chương trình chạy không quá 2 giây.
Kết quả xuất ra file văn bản TANSO.OUT gồm nhiều dòng. Mỗi dòng chứa 2 số Ai và Ki ghi cách nhau ít nhất một dấu cách trống. Trong đó Ai là số thuộc dãy, Ki là tần số của số Ai. Ai được xếp tăng dần từ đầu đến cuối file.

Câu 1.
\(y = \dfrac{{n + \sin 2n}}{{n + 5}} = \dfrac{{\dfrac{n}{n} + \dfrac{{\sin 2n}}{n}}}{{\dfrac{n}{n} + \dfrac{5}{n}}} = \dfrac{{1 + \dfrac{{2.\sin 2n}}{{2n}}}}{{1 + \dfrac{5}{n}}}\\ \Rightarrow \lim y = \dfrac{{1 + 0}}{{1 + 0}} = 1 \)
Câu 2.
\(\lim \dfrac{{3\sin n + 4\cos n}}{{n + 1}}\)
Vì \( - 1 \le \sin n \le 1; - 1 \le \cos n \le 1 \Rightarrow \) khi \(x \to \infty \) thì \(3\sin n + 4{\mathop{\rm cosn}\nolimits} = const \)
\(\Rightarrow T = \lim \dfrac{{3\sin n + 4\cos n}}{{n + 1}} = 0 \)
Chú thích: $const$ là kí hiệu hằng số, giống như dạng giới hạn L/vô cùng.

Đáp án D sai
Hàm đa thức có giới hạn tại mọi điểm và tại tất cả các điểm thì giới hạn trái luôn bằng giới hạn phải
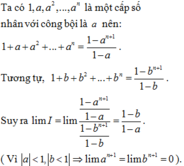
Chọn C.
Ta có 1, a, a2, …, an là một cấp số nhân công bội a nên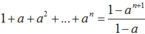
Tương tự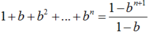
Suy ra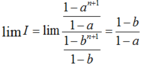
( Vì |a| < 1; |b| < 1). ⇒ liman+1 = limbn+1 = 0.