Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn phương án (D) :
Quỹ tích các điểm M nhìn đoạn thẳng AB dưới 1 góc \(120^0\) là hai cung chứa góc \(120^0\) (đối xứng nhau) dựng trên hai điểm A, B.
Chọn (D) hai cung chứa góc 120° (đối xứng nhau) dựng trên hai điểm A, B).
A B C D E M J O I
a) Ta có :
\(AC^2+BD^2=MA^2+MC^2+MB^2+MD^2\)
\(=\left(MA^2+MD^2\right)+\left(MB^2+MC^2\right)=AD^2+BC^2\)
Kẻ đường kính CE ta có \(\widehat{CDE}=90^0\) hay \(CD\perp DE\)
\(\Rightarrow DE//AB\)nên tứ giác ABED là hình thang cân
\(\Rightarrow AD=BE\)
Ta có : \(AD^2+BC^2=BE^2+BC^2=CE^2=4R^2\)không đổi
b ) \(IB=IC=IM\)nên \(IO^2+IM^2=OC^2-IM^2+IM^2=R^2\)
Gọi J là trung điểm của MO . Áp dụng công thức đường trung tuyến trong \(\Delta IMO\)
Ta có : \(IJ=\sqrt{\frac{IO^2+IM^2}{2}-\frac{MO^2}{4}}=\sqrt{\frac{R^2}{2}-\frac{MO^2}{4}}\)( không đổi vì O,M cố định )
Do đó I chạy trên đường tròn tâm J bán kính IJ không đổi.
Chúc bạn học tốt !!!
a. Ta có: \(\widehat{ADB}=90^o\)(góc nội tiếp chắn nửa đường tròn) => \(\widehat{ADE}=90^o\)
Lại có: \(CH\perp AB\)tại H (gt) mà E \(\in CH\)(do E là giao điểm của BD và CH (gt)) => \(\widehat{EHA}=90^o\)
Xét tứ giác ADEH có: \(\widehat{ADE}+\widehat{EHA}=90^o+90^o=180^o\)=> tứ giác ADEH nội tiếp (DHNB) => đpcm
b.
Ta có: \(\widehat{ACB}=90^o\)(góc nội tiếp chắn nữa đường tròn) => \(\Delta ABC\)vuông tại C
=> \(S\Delta ABC=\frac{1}{2}AC\times BC=\frac{1}{2}CH\times AB\)=> CH = \(\frac{AC\times BC}{AB}\)
=> \(AC\times AH+CB\times CH=AC\times AH+CB\times\frac{AC\times BC}{AB}\)= \(AC\times(AH+\frac{BC^2}{AB})=AC\times\frac{(AH\times AB+BC^2)}{AB}\)(1)
Áp dụng hệ thức lượng trong \(\Delta ABC\)vuông tại C với đường cao CH ta được: AH \(\times AB=AC^2\)(2)
Áp dụng định lý pitago trong \(\Delta ABC\)vuông tại C ta được: \(AC^2+BC^2=AB^2\)(3)
Thế (2) và (3) vào (1) ta được : \(AC\times AH+CB\times CH=AB\times AC\)(ĐPCM)
c. Gọi K là điểm chính giữa cung AB (K nằm cùng phía với C so với bờ AB) => K là điểm cố định và \(KO\perp AB\)tại O => KO // CH => \(\widehat{KOC}=\widehat{KOM}=\widehat{HCO}\)(So le trong)
Nối K với M
Xét \(\Delta KOM\)và \(\Delta OCH\)có:
+ KO = OC = R
+ \(\widehat{KOM}=\widehat{HCO}\)(cmt)
+ OM = CH (gt)
=> \(\Delta KOM=\Delta OCH\)(c.g.c) => \(\widehat{KMO}=\widehat{OHC}=90^o\Rightarrow\Delta KOM\)vuông tại M => M \(\in(I,\frac{OK}{2})\)cố định (trong đó I là trung điểm của OK)
Chọn đáp án B
Xét hình thoi ABCD có hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường
Suy ra AO ⊥ BO ⇒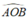
= 90°
Ta có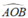
= 90° không đổi mà cố định
⇒ Quỹ tích điểm O là nửa đường tròn đường kính AB trừ hai điểm A và B