Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn trả lời:
a) Xét hai tam giác vuông AOC và BDO ta có: ˆA=ˆB=900A^=B^=900
ˆAOC=ˆBDOAOC^=BDO^ (hai góc có cạnh tương ứng vuông góc).
Vậy ∆AOC ~ ∆BDO
⇒ACAO=BOBDhayACa=bBD⇒ACAO=BOBDhayACa=bBD (1)
Vậy AC . BD = a . b = không đổi.
b) Khi thì tam giác AOC trở thành nửa tam giác đều cạnh là OC, chiều cao AC.
⇒OC=2AO=2a⇔AC=OC√32=a√3⇒OC=2AO=2a⇔AC=OC32=a3
Thay AC = a√3 vào (1), ta có:
ACa=bBD=a√3.BD=a.b⇒BD=aba√3=b√33ACa=bBD=a3.BD=a.b⇒BD=aba3=b33
Ta có công thức tính diện tích hình thang ABCD là:
S=AC+BD2.AB=a√3+b√332.(a+b)=√36(3a2+4ab+b2)(cm2)S=AC+BD2.AB=a3+b332.(a+b)=36(3a2+4ab+b2)(cm2)
c) Theo đề bài ta có:
∆AOC tạo nên hình nón có bán kính đáy là AC = a√3 và chiều cao là AO = a.
∆BOD tạo nên hình nón có bán kính đáy là BD=b√33BD=b33 và chiều cao OB = b
Ta có: V1V2=13π.AC2.AO13π.BD2.OB=AC2.AOBD2.OB=(a√3)2.a(b√33)2.b=3a3b33=9a3b3V1V2=13π.AC2.AO13π.BD2.OB=AC2.AOBD2.OB=(a3)2.a(b33)2.b=3a3b33=9a3b3
Vậy V1V2=9a3b3



c) Khi quay hình vẽ xung quanh cạnh AB: ΔAOC tạo nên hình nón, bán kính đáy là AC, chiều cao AO; ΔBOD tạo nên hình nón, bán kính đáy BD, chiều cao OB.


Khi quay hình vẽ xung quanh cạnh AB: ΔAOC tạo nên hình nón, bán kính đáy là AC, chiều cao AO; ΔBOD tạo nên hình nón, bán kính đáy BD, chiều cao OB.


Giải:
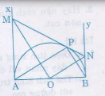
a) Ta có OM, ON lần lượt là tia phân giác cả AOP và BOP
Mà AOP kể bù BOP nên suy ra OM vuông góc với ON.
Vậy ∆MON vuông tại O.
Lại có ∆APB vuông vì có góc vuông (góc nội tiếp chắn nửa cung tròn)
Tứ giác AOPM nội tiếp đường tròn vì có +
= 2v. Nên
=
(cùng chắn cung OP).
Vậy hai tam giác vuông MON à APB đồng dạng vị có cắp góc nhọn bằng nhau.
b)
Tam giác AM = MP, BN = NP (1) (tính chất hai tiếp tuyến cắt nhau)
Tam giác vuông MON có OP là đường cao nên:
MN.PN = OP2 (2)
Từ 1 và 2 suy ra AM.BN = OP2 = R2
c) Từ tam giác MON đồng dạng với tam giác APB ta có :
Khi AM = thi do AM.BN = R2 suy ra BN = 2R
Do đó MN = MP + PN = AM + BN = + 2R =
Suy ra MN2 =
Vậy =
d) Nửa hình tròn APB quay quanh bán kính AB = 2R sinh ra một hình cầu có bán kính R.
Vậy V = πR3
-0131.jpg)
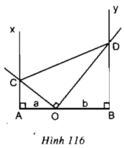
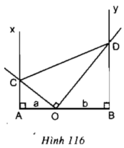
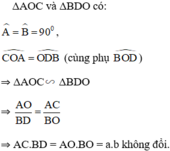


a, A O C ^ = O D B ^ (cùng phụ B O D ^ )
=> DAOC ~ DBDO (g.g)
=> A C B O = A O B D
=> AC.BD = a.b (không đổi)
b, Ta có C O A ^ = O D B ^ = 60 0 , A C O ^ = D O B ^ = 30 0 , AC = a 3 , BD = b 3 3
i, S A B C D = 3 a + b 3 a + b 6
ii, 9