
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

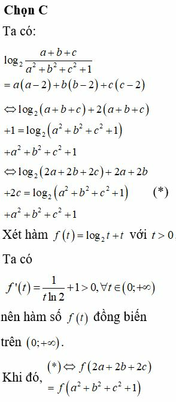
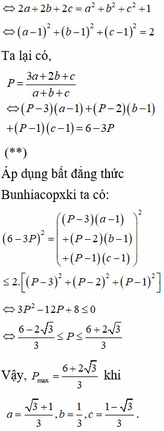

Ta có : \(\sqrt{\frac{ab}{ab+2c}}=\sqrt{\frac{ab}{ab+\left(a+b+c\right)c}}=\sqrt{\frac{ab}{\left(a+c\right)\left(b+c\right)}}\le\frac{1}{2}\left(\frac{a}{a+c}+\frac{b}{b+c}\right)\)
Đẳng thức xảy ra khi và chỉ khi \(\frac{a}{a+c}+\frac{b}{b+c}\)
Tương tự ta cũng có
\(\sqrt{\frac{bc}{bc+2a}}\le\frac{1}{2}\left(\frac{b}{b+a}+\frac{c}{c+a}\right);\sqrt{\frac{ca}{ca+2b}}\le\frac{1}{2}\left(\frac{c}{c+a}+\frac{a}{a+b}\right)\)
Cộng các vế ta được \(S\le\frac{1}{2}\left(\frac{a+b}{a+b}+\frac{b+c}{b+c}+\frac{c+a}{c+a}\right)=\frac{3}{2}\)
Đẳng thức xảy ra khi và chỉ khi \(a=b=c=\frac{2}{3}\)
Vậy \(S_{max}=\frac{3}{2}\Leftrightarrow x=y=z=\frac{2}{3}\)

\(\left\{{}\begin{matrix}x^2=2log_a\left(ab\right)=2\left(1+log_ab\right)\\y^2=2log_b\left(ab\right)=2\left(1+log_ba\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2log_ab=x^2-2\\2log_ba=y^2-2\end{matrix}\right.\) \(\Rightarrow\left(x^2-2\right)\left(y^2-2\right)=4\)
\(\Leftrightarrow y^2-2=\frac{4}{x^2-2}\Rightarrow y^2=\frac{2x^2}{x^2-2}\) (\(x\ge\sqrt{2}\))
\(\Rightarrow P=f\left(x\right)=8x+\frac{x\sqrt{2}}{\sqrt{x^2-2}}=0\)
\(\Rightarrow f'\left(x\right)=8-\frac{2\sqrt{2}x}{\left(x^2-2\right)^2\sqrt{\frac{x^2}{x^2-2}}}=0\)
\(\Leftrightarrow\left(x^2-2\right)^3=\frac{1}{8}\Leftrightarrow x^2-2=\frac{1}{2}\Rightarrow x=\frac{\sqrt{10}}{2}\)
\(\Rightarrow P_{min}=P\left(\frac{\sqrt{10}}{2}\right)=5\sqrt{10}\Rightarrow\left\{{}\begin{matrix}m=0\\n=5\\m=10\end{matrix}\right.\) \(\Rightarrow m+n+p=15\)

Bạn ơi có thể hướng dẫn chi tiết giúp mình không? cám ơn nhiều ạ