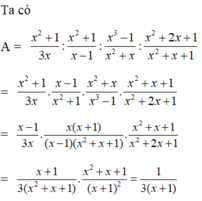Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, \(\dfrac{x^2-x}{x-2}+\dfrac{4-3x}{x-2}\)
\(=\dfrac{x^2-x+4-3x}{x-2}=\dfrac{x^2-4x+4}{x-2}\)
c) \(\dfrac{2}{x^2-9}+\dfrac{1}{x+3}\)
Ta có: \(\dfrac{1}{x+3}=\dfrac{1\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{x-3}{x^2-9}\)
\(\Rightarrow\dfrac{2}{x^2-9}+\dfrac{1}{x+3}=\dfrac{2}{x^2-9}+\dfrac{x-3}{x^2-9}=\dfrac{2+x-3}{x^2-9}=\dfrac{x-1}{x^2-9}\)

1.
a, \(\left(x+3\right)\left(x-3\right)-\left(x-3\right)^2\)
\(=\left(x-3\right)\left(x+3-x+3\right)\)
\(=9\left(x-3\right)=9x-27\)
b, \(\left(2x+1\right)^2+2\left(2x+1\right)\left(x-1\right)+\left(x-1\right)^2\)
\(=\left(2x+1+x-1\right)^2=9x^2\)
c, \(x\left(x-3\right)\left(x+3\right)-\left(x^2+1\right)\left(x^2-1\right)\)
\(=x\left(x^2-9\right)-\left(x^4-1\right)\)
\(=x^3-9x-x^4+1=-x^4+x^3-9x+1\)

A=(\(\frac{x^3-1}{x\left(x-1\right)}\)-\(\frac{x^3-1}{x\left(x+1\right)}\)) : \(\frac{2\left(x^2-2x+1\right)}{\left(x-1\right)\left(x+1\right)}\)ĐKXĐ: x\(\ne\) -1, 1
A=\(\frac{1}{x\left(x+1\right)}\)x \(\frac{\left(x-1\right)\left(x+1\right)}{2\left(x-1\right)\left(x-1\right)}\)
A=\(\frac{1}{2x^2-2x}\)
B=\(\frac{x+1}{x-2}\)-\(\frac{2x}{x+2}\)-\(\frac{2+5x}{x^2-4}\)ĐKXĐ : x\(\ne\)2, -2
B=\(\frac{x+1}{x-2_{ }}\)-\(\frac{2x}{x+2}\)-\(\frac{2+5x}{\left(x-2\right)\left(x+2\right)}\)
B=\(\frac{x^2+3x+2}{\left(x-2\right)\left(x+2\right)}\)-\(\frac{2x^2-4x}{\left(x-2\right)\left(x+2\right)}\)-\(\frac{2+5x}{\left(x-2\right)\left(x+2\right)}\)
B=\(\frac{-x^2+2x}{\left(x-2\right)\left(x+2\right)}\)
B=\(\frac{-x\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
B=\(\frac{-x}{x+2}\)

d) \(\dfrac{x+1}{x-1}-\dfrac{x+2}{x+3}+\dfrac{4}{x^2+2x-3}=0\) (ĐKXĐ: \(x\ne1;-3\))
\(\Leftrightarrow\dfrac{\left(x+1\right)\left(x+3\right)-\left(x+2\right)\left(x-1\right)+4}{\left(x+3\right)\left(x-1\right)}=0\)
\(\Rightarrow\left(x+1\right)\left(x+3\right)-\left(x+2\right)\left(x-1\right)+4=0\)
\(\Leftrightarrow x^2+4x+3-x^2-x+2+4=0\)
\(\Leftrightarrow3x+9=0\Leftrightarrow x=-3\left(loại\right)\)
vậy phương trình đã cho vô nghiệm
c)\(\dfrac{2}{x-1}-\dfrac{3x^2}{x^3-1}=\dfrac{x}{x^2+x+1}\) (ĐKXĐ: \(x\ne1\))
\(\Leftrightarrow\dfrac{2\left(x^2+x+1\right)-3x^2}{x^3-1}=\dfrac{x\left(x-1\right)}{x^3-1}\)
\(\Rightarrow2x^2+2x+2-3x^2=x^2-x\)
\(-2x^2+3x+2=0\)
\(\left(x-2\right)\left(-2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\Leftrightarrow x=2\\-2x-1=0\Leftrightarrow x=-\dfrac{1}{2}\end{matrix}\right.\)
vậy tập nghiệm của phương trình là S={2;-0,5)

a)
\(x(x+1)-(x+2)(x-3)=7\)
\(\Leftrightarrow (x^2+x)-(x^2-x-6)=7\)
\(\Leftrightarrow 2x+6=7\Leftrightarrow 2x=1\Leftrightarrow x=\frac{1}{2}\)
b) ĐK: \(x\neq \pm 1\)
\(\frac{x-3}{x+1}=\frac{x^2}{x^2-1}\Leftrightarrow \frac{(x-3)(x-1)}{(x+1)(x-1)}=\frac{x^2}{x^2-1}\)
\(\Leftrightarrow \frac{x^2-4x+3}{x^2-1}=\frac{x^2}{x^2-1}\)
\(\Rightarrow x^2-4x+3=x^2\)
\(\Leftrightarrow -4x+3=0\Leftrightarrow x=\frac{3}{4}\) (t/m)
c) ĐK: \(x\neq -2; x\neq 3\)
\(\frac{1}{x+2}-\frac{4}{x-3}=\frac{10}{(x+2)(x-3)}\)
\(\Leftrightarrow \frac{x-3-4(x+2)}{(x+2)(x-3)}=\frac{10}{(x+2)(x-3)}\)
\(\Rightarrow x-3-4(x+2)=10\)
\(\Leftrightarrow -3x-21=0\Leftrightarrow x=-7\) (t/m)
d) ĐK: \(x\neq \pm 2\)
\(\frac{1}{x-2}+\frac{x-3}{x+2}=1\)
\(\Leftrightarrow \frac{x+2+(x-3)(x-2)}{(x-2)(x+2)}=1\)
\(\Rightarrow x+2+(x-3)(x-2)=(x-2)(x+2)\)
\(\Leftrightarrow x^2-4x+8=x^2-4\)
\(\Leftrightarrow -4x=-12\Leftrightarrow x=3\) (t.m)