Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(y=8x^4+ax^2+b\Rightarrow y'=32x^3+2ax\)
\(y'=0\Rightarrow2x\left(16x^2+a\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x^2=-\frac{a}{16}\end{matrix}\right.\)
- Nếu \(a>0\Rightarrow y'=0\) có đúng 1 nghiệm \(x=0\)
\(\Rightarrow f\left(x\right)_{max}=f\left(-1\right)=f\left(1\right)=\left|a+b+8\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=-7\\a+b=-9\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}b=-7-a< 0\\b=-9-a< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a>0\\b< 0\end{matrix}\right.\)
Đáp án A đúng luôn, ko cần xét \(a< 0\) nữa

a) f(x) = 2x3 – 3x2 – 12x + 1 ⇒ f’(x) = 6x2 – 6x – 12
f’(x) = 0 ⇔ x ∈ {-1, 2}
So sánh các giá trị:
f(x) = -3; f(-1) = 8;
f(2) = -19, f(52)=−332f(52)=−332
Suy ra:
maxx∈[−2,52]f(x)=f(−1)=8minx∈[−2,52]f(x)=f(2)=−19maxx∈[−2,52]f(x)=f(−1)=8minx∈[−2,52]f(x)=f(2)=−19
b) f(x) = x2 lnx ⇒ f’(x)= 2xlnx + x > 0, ∀ x ∈ [1, e] nên f(x) đồng biến.
Do đó:
maxx∈[1,e]f(x)=f(e)=e2minx∈[1,e]f(x)=f(1)=0maxx∈[1,e]f(x)=f(e)=e2minx∈[1,e]f(x)=f(1)=0
c) f(x) = f(x) = xe-x ⇒ f’(x)= e-x – xe-x = (1 – x)e-x nên:
f’(x) = 0 ⇔ x = 1, f’(x) > 0, ∀x ∈ (0, 1) và f’(x) < 0, ∀x ∈ (1, +∞)
nên:
maxx∈[0,+∞)f(x)=f(1)=1emaxx∈[0,+∞)f(x)=f(1)=1e
Ngoài ra f(x) = xe-x > 0, ∀ x ∈ (0, +∞) và f(0) = 0 suy ra
maxx∈[0,+∞)f(x)=f(0)=0maxx∈[0,+∞)f(x)=f(0)=0
d) f(x) = 2sinx + sin2x ⇒ f’(x)= 2cosx + 2cos2x
f’(x) = 0 ⇔ cos 2x = -cosx ⇔ 2x = ± (π – x) + k2π
⇔ x∈{−π+k2π;π3+k2π3}x∈{−π+k2π;π3+k2π3}
Trong khoảng [0,3π2][0,3π2] , phương trình f’(x) = 0 chỉ có hai nghiệm là x1=π3;x2=πx1=π3;x2=π
So sánh bốn giá trị : f(0) = 0; f(π3)=3√32;f(π)=0;f(3π2)=−2f(π3)=332;f(π)=0;f(3π2)=−2
Suy ra:
maxx∈[0,3π2]f(x)=f(π3)=3√32minx∈[0,3π2]f(x)=f(3π2)=−2

a) Ta có tập xác định của cả hai hàm số \(f\left(x\right),g\left(x\right)\) đểu là \(\mathbb{R}\)
Mặt khác:
\(f\left(-x\right)=\dfrac{a^{-x}+a^{-x}}{2}=f\left(x\right);g\left(x\right)=\dfrac{a^{-x}-a^x}{2}=-g\left(x\right)\)
Vậy \(f\left(x\right)\) là hàm số chẵn, \(g\left(x\right)\) làm hàm số lẻ
b) Ta có :
\(f\left(x\right)=\dfrac{a^x+a^{-x}}{2}\ge\sqrt{a^xa^{-x}}=1,\forall x\in\mathbb{R}\)
và :
\(f\left(0\right)=\dfrac{a^0+a^0}{2}=1\)
Vậy :
\(minf\left(x\right)=f\left(0\right)=1\)

Chọn C.
Đặt t = f ( x ) → d t = f ' x d x . Đổi cận: x = 2016 → t = f ( 2016 ) = a x = 2017 → t = f ( 2017 ) = b
Khi đó
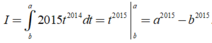

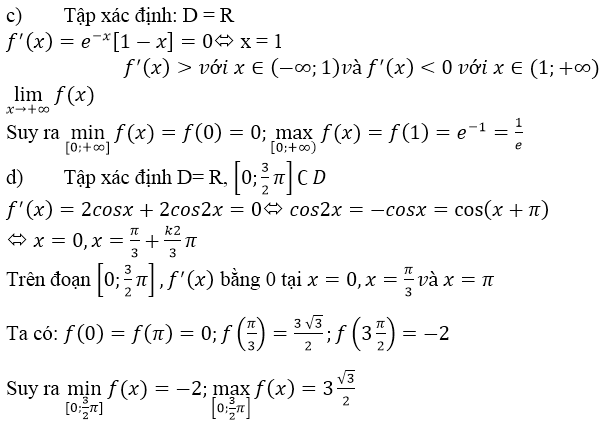
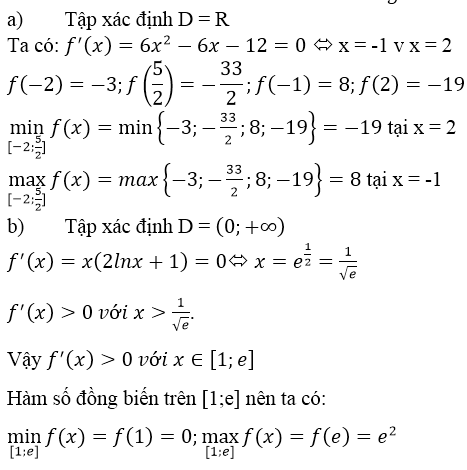
Chọn A
Hàm số y = f(x) thỏa mãn f'(x) < 0 ∀ x ∈ ( a ; b ) nên hàm số nghịch biến trên (a;b).
Do đó