Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kiến thức áp dụng
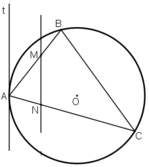
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.

Ta có 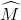 =
= 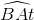 (so le trong) (1)
(so le trong) (1)
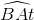 =
= 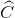 (2)
(2)
( là góc tạo bởi tiếp tuyến và dây cung, chắn cung AB, 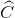 là góc nội tiếp chắn cung AB)
là góc nội tiếp chắn cung AB)
Từ (1) và (2) suy ra:
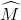 =
= 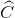 (3)
(3)
Xét hai tam giác AMN và ACB. chúng có:
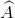 chung
chung
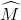 =
= 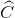
Vậy ∆AMN ~ ∆ACB, từ đó 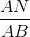 =
= 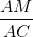 , suy ra AB. AM = AC . AN
, suy ra AB. AM = AC . AN

Xét ΔANM và ΔABC có
góc ANM=góc ABC(=1/2sđ cung AC)
góc NAM chung
=>ΔANM đồng dạng với ΔABC
=>AN/AB=AM/AC
=>AN*AC=AB*AM

a: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>\(\widehat{BAC}=90^0\)
Xét ΔABC có
O là trung điểm của BC
OD//AC
Do đó: D là trung điểm của AB
b:
Ta có: ΔOAB cân tại O
mà OD là đường trung tuyến
nên OD\(\perp\)AB
=>OE\(\perp\)AB tại D
ΔOAB cân tại O
mà OE là đường cao(OE\(\perp\)AB tại D
nên OE là phân giác của \(\widehat{AOB}\)
=>\(\widehat{AOE}=\widehat{BOE}\)
Xét ΔOBE và ΔOAE có
OB=OA
\(\widehat{BOE}=\widehat{AOE}\)
OE chung
Do đó: ΔOBE=ΔOAE
=>\(\widehat{OBE}=\widehat{OAE}=90^0\)
=>EA là tiếp tuyến của (O)
c:Ta có: OE\(\perp\)AB
AB\(\perp\)AC
Do đó: OE//AC
Xét ΔFBC có
O là trung điểm của BC
OE//FC
Do đó: E là trung điểm của BF
+ B A t ^ là góc tạo bởi tiếp tuyến at và dây AB B C A ^ là góc nội tiếp chắc cung nhỏ B A ⏜