
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

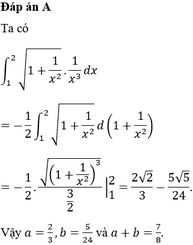

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

a) (n + 2) chia hết cho (n - 1). \(\left(n\in N\right)\)
\(\Rightarrow\) n - 2 + 4 chia hết cho n - 1
\(\Rightarrow\) 4 chia hết cho n - 1
\(\Rightarrow\) n - 1 \(\in\) Ư(4) = {1; 2; 4;}
\(\Rightarrow\) n \(\in\) {2; 3; 5}
b) (2n + 7) chia hết cho (n + 1). \(\left(n\in N\right)\)
\(\Rightarrow\) 2n + 2 + 5 chia hết cho n + 1
\(\Rightarrow\) 2(n + 1) + 5 chia hết cho n + 1
\(\Rightarrow\) 5 chia hết cho n + 1
\(\Rightarrow\) n + 1 \(\in\) Ư(5) = {1; 5;}
\(\Rightarrow\) n \(\in\) {0; 4}
c) (2n + 1) chia hết cho (6 - n). \(\left(n\in N\right)\)
\(\Rightarrow\) (12 - 2n) - (12 - n) + (2n + 1) chia hết cho 6 - n
\(\Rightarrow\) 2(6 - n) - 12 + n + 2n + 1 chia hết cho 6 - n
\(\Rightarrow\) -12 + 3n + 1 chia hết cho 6 - n
\(\Rightarrow\) 18 - 3n - 12 + 1 chia hết cho 6 - n
\(\Rightarrow\) 3(6 - n) - 12 + 1 chia hết cho 6 - n
\(\Rightarrow\) -11 chia hết cho 6 - n
\(\Rightarrow\) 6 - n \(\in\) Ư(-11) = {-1; 1; -11; 11}
\(\Rightarrow\) Không có số tự nhiên n thỏa mãn
d) 3n chia hết cho (5 - 2n) \(\left(n\in N\right)\)
\(\Rightarrow\) 3n chia hết cho 5 - n - n
\(\Rightarrow\) 15 - 4n - 4n chia hết cho 5 - n - n
\(\Rightarrow\) 3(5 - n - n) chia hết cho 5 - n - n
KL: Theo đề bài, ta có \(\left(n\in N\right)\) sao cho 3n chia hết cho (5 - 2n) và 2n < 5
\(\Rightarrow\) n \(\in\) {0; 1; 2}
e) (4n + 3) chia hết cho (2n + 6) \(\left(n\in N\right)\)
\(\Rightarrow\) (2n + 6) + (2n + 6) - 9 chia hết cho 2n + 6
\(\Rightarrow\) 2(2n + 6) - 9 chia hết cho 2n + 6
\(\Rightarrow\) - 9 chia hết cho 2n + 6
\(\Rightarrow\) 2n + 6 \(\in\) Ư(-9) = {-1; 1; -3; 3; -9; 9}
\(\Rightarrow\) Không có số tự nhiên n thỏa mãn
a) (n + 2) chia hết cho (n - 1). \(\left(n\in N\right)\)
\(\Rightarrow\) n - 2 + 4 chia hết cho n - 1
\(\Rightarrow\) 4 chia hết cho n - 1
\(\Rightarrow\) n - 1 \(\in\) Ư(4) = {1; 2; 4;}
\(\Rightarrow\) n \(\in\) {2; 3; 5}
b) (2n + 7) chia hết cho (n + 1). \(\left(n\in N\right)\)
\(\Rightarrow\) 2n + 2 + 5 chia hết cho n + 1
\(\Rightarrow\) 2(n + 1) + 5 chia hết cho n + 1
\(\Rightarrow\) 5 chia hết cho n + 1
\(\Rightarrow\) n + 1 \(\in\) Ư(5) = {1; 5;}
\(\Rightarrow\) n \(\in\) {0; 4}
c) (2n + 1) chia hết cho (6 - n). \(\left(n\in N\right)\)
\(\Rightarrow\) (12 - 2n) - (12 - n) + (2n + 1) chia hết cho 6 - n
\(\Rightarrow\) 2(6 - n) - 12 + n + 2n + 1 chia hết cho 6 - n
\(\Rightarrow\) -12 + 3n + 1 chia hết cho 6 - n
\(\Rightarrow\) 18 - 3n - 12 + 1 chia hết cho 6 - n
\(\Rightarrow\) 3(6 - n) - 12 + 1 chia hết cho 6 - n
\(\Rightarrow\) -11 chia hết cho 6 - n
\(\Rightarrow\) 6 - n \(\in\) Ư(-11) = {-1; 1; -11; 11}
\(\Rightarrow\) Không có số tự nhiên n thỏa mãn
d) 3n chia hết cho (5 - 2n) \(\left(n\in N\right)\)
\(\Rightarrow\) 3n chia hết cho 5 - n - n
\(\Rightarrow\) 15 - 4n - 4n chia hết cho 5 - n - n
\(\Rightarrow\) 3(5 - n - n) chia hết cho 5 - n - n
KL: Theo đề bài, ta có \(\left(n\in N\right)\) sao cho 3n chia hết cho (5 - 2n) và 2n < 5
\(\Rightarrow\) n \(\in\) {0; 1; 2}
e) (4n + 3) chia hết cho (2n + 6) \(\left(n\in N\right)\)
\(\Rightarrow\) (2n + 6) + (2n + 6) - 9 chia hết cho 2n + 6
\(\Rightarrow\) 2(2n + 6) - 9 chia hết cho 2n + 6
\(\Rightarrow\) - 9 chia hết cho 2n + 6
\(\Rightarrow\) 2n + 6 \(\in\) Ư(-9) = {-1; 1; -3; 3; -9; 9}
\(\Rightarrow\) Không có số tự nhiên n thỏa mãn

Câu 1 : Việc gõ ký hiệu như bạn đề cập ; mình cũng không biết phải làm sao nên cứ dùng xyz vậy thôi.
Ta có:
xyz = 100x +10y +z = 111x -11x +10y +z = 37.3x -(11x-10y-z) chia hết cho 37
=> (11x-10y-z) chia hết cho 37
Lại có:
xyz -yzx = 100x +10y +z -100y -10z -x = 99x -90y -9z = 9.(11x-10y-z) chia hết cho 37
Vậy yzx cũng phải chia hết cho 37
Có thể phát biểu hay hơn là CMR: Khi hoán vị các chữ số của 1 số có 3 chữ số chia hết cho 37 thì được số mới cũng chia hết cho 37.

\(x^{15}-\left(7+1\right)x^{14}+\left(7+1\right)x^{13}....+\left(7+1\right)x-5\)
\(=x^{15}-\left(x+1\right)x^{14}+\left(x+1\right)x^{13}....+\left(x+1\right)x-5\)
\(=x^{15}-x^{15}-x^{14}+x^{14}+x^{13}....-x^3-x^2+x^2+x-5\)
\(=x-5=7-5=2\)

* Sửa:
a) 35 - (-x + 8) = 23 - (-7)
35 + x - 8 = 30
35 + x = 30 + 8
35 + x = 38
x = 38 - 35
x = 3
Vậy, x = 3
b) 4 - 2(x - 3) = 3 (3 - x)
4 - (2x - 2 . 3) = 3 . 3 - 3x
4 - (2x - 6) = 9 - (2x + x)
4 - 2x + 6 = 9 - 2x - x
(4 + 6) = 9 - x
10 = 9 - x
9 - 10 = x
-1 = x
x = -1
Vậy, x = -1

ta có \(\left|x-a\right|+\left|x-b\right|+\left|x-c\right|+\left|x-d\right|\ge\left|\left(x-a\right)+\left(x-b\right)+\left(c-x\right)+\left(d-x\right)\right|=\left|c+d-a-b\right|=c+d-a-b\)( do a<b<c<d => c-a>0 và d-b>0)
vậy Min A= c+d-a-b

Bài 2:
a) Ta có:
\(S=1-3+3^2-3^3+3^4-3^5+3^6-3^7+...+3^{96}-3^{97}+3^{98}-3^{99}\)
\(=\left(1-3+3^2-3^3\right)+\left(3^4-3^5+3^6-3^7\right)+...+\left(3^{96}-3^{97}+3^{98}-3^{99}\right)\)
\(=1.\left(1-3+3^2-3^3\right)+3^4.\left(1-3+3^2-3^3\right)+...+3^{96}.\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(-20\right)\) \(\text{⋮}\) \(-20\)
Vậy \(S\) \(\text{⋮}\) \(-20\)
Bài 1:
Ta có:
\(A=\left(5m^2-8m^2-9m^2\right).\left(-n^3+4n^3\right)\)
\(=\left[\left(5-8-9\right).m^2\right].\left[\left(-1+4\right).n^3\right]\)
\(=\left(-12\right).m^2.3.n^3\)
\(=\left(m^2.3\right).\left[\left(-12\right)n^3\right]\)
Xét: \(m^2\ge0\) với V m
3>0 nên \(m^2.3\ge0\) với V m
Như vậy để \(A\ge0\) thì \(\left(-12\right)n^3\ge0\)
-12 < 0 nên nếu \(\left(-12\right)n^3\ge0\) thì \(n^3<0\Rightarrow n<0\)
Vậy với n<0 và mọi m thì \(A\ge0\)