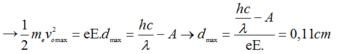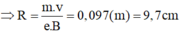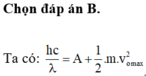Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: B
Sử dụng phương trình Anhxtanh ta được:
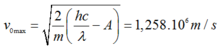
Khi chuyển động trong điện trường đều và từ trường hướng vuông góc với nhau, e chuyển động thẳng đều khi lực điện cân bằng với lực lorenxo khi đó ta có:
e.vmaxB = e.E
→E = 1258V/m

Electron chuyển động đều tức là lực điện cân bằng với lực từ:
\(F_E=F_B\)
\(\Rightarrow eE=evB\)
\(\Rightarrow v=\frac{E}{B}=10^6\left(\text{m/s}\right)\)
Động năng của electron:
\(T=\frac{m_ev^2}{2}\)
Năng lượng của photon cung cấp công thoát cho electron và cho electron vận tốc đầu (động năng):
\(h\frac{c}{\lambda}\text{=}E_{th}+T\) (\(E_{th}\)là công thoát)
\(\lambda=\frac{hc}{E_{th}+T}=1,7.10^{-7}\left(m\right)=0,17\left(nm\right)\)
\(chọn.A\)

Câu trả lời ở đây bạn nhé
Câu hỏi của lý - Học và thi online với HOC24

Từ hệ thức Anh-xtanh ta có:
_ Với bức xạ \(\lambda_1:\)\(\frac{hc}{\lambda}=A+\frac{1}{2}mv^2_1\left(1\right)\)
_Với bức xạ \(\lambda_2:\)\(\frac{hc}{\lambda_2}=A+\frac{1}{2}mv^2_2\left(2\right)\)
Từ (1) và (2) \(\Rightarrow m_e=\frac{2hc}{v^1_2-v^2_2}\left(\frac{1}{\lambda_1}-\frac{1}{\lambda_2}\right)\)
![]()
ừ hệ thức Anh-xtanh ta có:
_ Với bức xạ λ1:hcλ=A+12mv21(1)λ1:hcλ=A+12mv12(1)
_Với bức xạ λ2:hcλ2=A+12mv22(2)λ2:hcλ2=A+12mv22(2)
Từ (1) và (2) ⇒me=2hcv21−v22(1λ1−1λ2)⇒me=2hcv12−v22(1λ1−1λ2).

Đáp án B
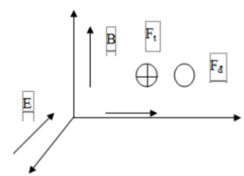
Phương pháp: sử dụng quy tắc bàn tay trái, hai lực cân bằng, lực điện
Cách giải:
Áp dụng quy tắc bàn tay trái thì nhận thấy lực từ tác dụng lên hạt có phương của Oy và có chiều ngược Oy. Mà do hạt vẫn giữ nguyên phương vận tốc Ox, nên lực điện phải cân bằng với lực từ. Lực điện có phương Oy và cùng chiều Oy,
Ta có lực điện F = q.E
Vì hạt mang điện âm nên có lực điện có chiều ngược với chiều của E. vậy E có phương Oy và chiều ngược với Oy.
Áp dụng công thức Anhxtanh về hiện tượng quang điện ta tìm được vận tốc của hạt
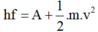
Từ đó áp dụng công thức tính lực điện và lực từ và cho hai lực bằng nhau về độ lớn ta tìm được E =>
![]()

Đáp án: D
Áp dụng định lý biến thiên động năng ta có:
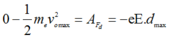
(vì lực điện trường tác dụng lên e có chiều ngược với chiều điện trường)
dmax là quãng đường tối đa mà vật đi được trong điện trường.