PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1
18 tháng 4 2016
S D A H B M C I N
Gọi H là tâm của ABCD\(\Rightarrow SH\perp\left(ABCD\right)\)
M là trung điểm của BC \(\Rightarrow BC\perp\left(SHM\right)\)
Do các mặt bên tạo với đáy cùng 1 góc => \(\widehat{SHM}\) bằng góc tạo bởi 2 mặt bên với đáy
Tính được \(SH=\frac{a\sqrt{3}}{2}'HM=\frac{a}{2}\)
\(\tan\widehat{SMH}=\frac{SH}{MH}=\sqrt{3}\Rightarrow\widehat{SMN}=60^0\)
Lập luận được tâm khối cầu là điểm I của SH với trung trực SC trong (SHC)
Tính được bán kính khối cầu do tam giác SNI đồng dạng với tam giác SHC
\(\Rightarrow SI=\frac{SN.SC}{SH}=\frac{5a}{4\sqrt{3}}\)
Vậy \(V=\frac{4}{3}\pi R^2=\frac{125a^3\sqrt{3}\pi}{432}\)
CM
24 tháng 5 2017
Chọn C.
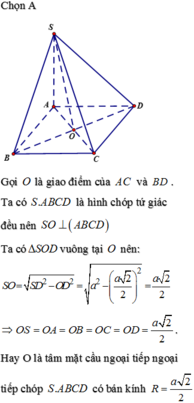
Điều kiện để hình chóp nội tiếp được trong một mặt cầu là đáy của nó nội tiếp trong một đường tròn. Một tứ giác bất kì chưa chắc nội tiếp trong một đường tròn.
1 tháng 10 2021
Chọn C vì điều kiện để hình chóp nội tiếp được trong một mặt cầu là đáy của nó nội tiếp trong một đường tròn. Một tứ giác bất kì chưa chắc nội tiếp trong một đường tròn.
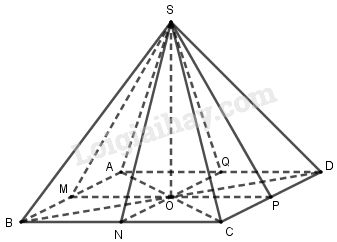
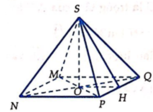
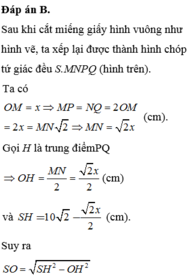
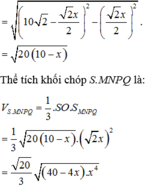
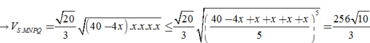
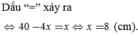
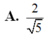
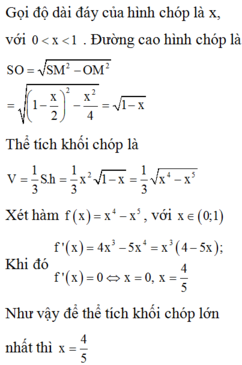
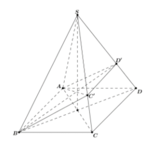
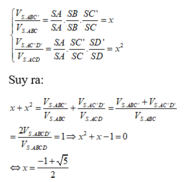
Cho hình chóp tứ giác đều S.ABCD. Hai đường chéo AC, BD và hai đường thẳng nối trung điểm các cặp cạnh đối diện của hình vuông ABCD chia hình vuông ABCD thành tám tam giác bằng nhau. Xem mỗi tam giác đó là đáy của một hình chóp đỉnh S ta sẽ được tám hình chóp bằng nhau.