Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Ta có : \(\frac{2016a+b+c+d}{a}=\frac{a+2016b+c+d}{b}=\frac{a+b+2016c+d}{c}=\frac{a+b+c+2016d}{d}\)
Trừ 4 vế với 2015 ta được : \(\frac{a+b+c+d}{a}=\frac{a+b+c+d}{b}=\frac{a+b+c+d}{c}=\frac{a+b+c+d}{d}\)
Nếu a + b + c + d = 0
=> a + b = -(c + d)
=> b + c = (-a + d)
=> c + d = -(a + b)
=> d + a = (-b + c)
Khi đó M = (-1) + (-1) + (-1) + (-1) = - 4
Nếu a + b + c + d\(\ne0\Rightarrow\frac{1}{a}=\frac{1}{b}=\frac{1}{c}=\frac{1}{d}\Rightarrow a=b=c=d\)
Khi đó M = 1 + 1 + 1 + 1 = 4
2) a) Ta có : \(\hept{\begin{cases}\left|x+2013\right|\ge0\forall x\\\left(3x-7\right)^{2004}\ge0\forall y\end{cases}\Rightarrow\left|x+2013\right|+\left(3x-7\right)^{2014}\ge0}\)
Dấu "=" xảy ra \(\hept{\begin{cases}x+2013=0\\3y-7=0\end{cases}\Rightarrow\hept{\begin{cases}x=-2013\\y=\frac{7}{3}\end{cases}}}\)
b) 72x + 72x + 3 = 344
=> 72x + 72x.73 = 344
=> 72x.(1 + 73) = 344
=> 72x = 1
=> 72x = 70
=> 2x = 0 => x = 0
c) Ta có :
\(\frac{7}{2x+2}=\frac{3}{2y-4}=\frac{5}{x+4}\Leftrightarrow\frac{7}{2x+2}=\frac{3}{2y-4}=\frac{10}{2x+8}=\frac{7-10}{2x+2-2x-8}=\frac{1}{2}\)(dãy tỉ số bằng nhau)
=> 2x + 2 = 14 => x = 6 ;
2y - 4 = 6 => y = 5 ;
6 + 5 + z = 17 => z = 6
Vậy x = 6 ; y = 5 ; z = 6
3) a) Ta có : \(\frac{a+b+c}{a+b-c}=\frac{a-b+c}{a-b-c}=\frac{a+b+c-a+b-c}{a+b-c-a+b+c}=\frac{2b}{2b}=1\)(dãy ti số bằng nhau)
=> a + b + c = a + b - c => a + b + c - a - b + c = 0 => 2c = 0 => c = 0;
Lại có : \(\frac{a+b+c}{a+b-c}-1=\frac{a-b+c}{a-b-c}-1\Leftrightarrow\frac{2c}{a+b-c}=\frac{2c}{a-b-c}\Rightarrow a+b-c=a-b-c\) => b = 0
Vậy c = 0 hoặc b = 0
c) Ta có : \(\frac{a+b}{c}=\frac{b+c}{a}=\frac{a+c}{b}=\frac{a+b+b+c+a+c}{c+a+b}=2\)(dãy tỉ số bằng nhau)
=> \(\hept{\begin{cases}a+b=2c\\b+c=2a\\a+c=2b\end{cases}}\)
Khi đó P = \(\left(1+\frac{c}{b}\right)\left(1+\frac{a}{c}\right)\left(1+\frac{b}{a}\right)=\frac{b+c}{b}.\frac{c+a}{c}=\frac{a+b}{a}=\frac{2a.2b.2c}{abc}=8\)
Vậy P = 8
2. b) \(7^{2x}+7^{2x+3}=344\)
\(7^{2x}\cdot\left(1+7^3\right)=344\)
\(7^{2x}\cdot\left(1+343\right)=344\)
\(7^{2x}\cdot344=344\)
\(7^{2x}=1\)
\(7^{2x}=7^0\)
\(2x=0\)
\(x=0\)

Câu 4:
a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB=DC
b: ta có: ABDC là hình bình hành
nên AB//DC
c: Xét hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
=>CB là tia phân giác của góc ACD

Cau a la 1
Cau b la 1215
Cau c la 768
Cau d la \(\frac{4185}{13}\)
\(\frac{4^2.4^3}{2^{10}}=\frac{4^{2+3}}{\left(2^2\right)^5}=\frac{4^5}{4^5}=1\)
\(\frac{\left(0,6\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2.3\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2\right)^5.3^5}{\left(0,2\right)^6}=\frac{3^5}{0,2}=1215\)
\(\frac{2^7.9^3}{6^5.8^2}=\frac{2^2.2^5.\left(3^2\right)^3}{\left(2.3\right)^5.\left(2^3\right)^2}=\frac{2^2.2^5.3^6}{2^5.3^5.2^6}=\frac{3}{2^4}=\frac{3}{16}\)
\(\frac{6^3+3.6^2+3^3}{-13}=\frac{2^3.3^3+3.\left(2.3\right)^2+3^3}{-13}=\frac{2^3.3^3+3.2^2.3^2+3^3}{-13}=\frac{3^3.\left(2^3+2^2+1\right)}{-13}=\frac{3^3.13}{-13}=\left(-3\right)^3=-27\)

ĐỀ 2
I. PHẦN TRẮC NGHIỆM: (3 điểm)
Khoanh tròn chữ cái đứng trước câu trả lời đúng:
1. Trong các khẳng định sau, khẳng định sai là:
A. I ⊂ R
B. I ∪ Q = R
C. Q ⊂ I
D. Q ⊂ R
2. Kết quả của phép nhân (-0,5)3.(-0,5) bằng:
A. (-0,5)3
B. (-0,5)
C. (-0,5)2
D. (0,5)4
3. Giá trị của (-2/3) ³ bằng:

=> Chọn B
4. Nếu | x | = |-9 |thì:
A. x = 9 hoặc x = -9
B. x = 9
B. x = -9
D. Không có giá trị nào của x để thỏa mãn
5. Kết quả của phép tính 36.34. 32 bằng:
A. 2712
B. 312
C. 348
D. 2748
=> 39168
6. Kết quả của phép tính ![]()

Câu 1:
Giải:
Ta có: \(15x=\left(-10\right)y=6z\Rightarrow\frac{15x}{30}=\frac{\left(-10\right)y}{30}=\frac{6z}{30}\Rightarrow\frac{x}{2}=\frac{y}{-3}=\frac{z}{5}\)
Đặt \(\frac{x}{2}=\frac{y}{-3}=\frac{z}{5}=k\)
\(\Rightarrow x=2k,y=-3k,z=5k\)
Mà \(xyz=-30000\)
\(\Rightarrow2k\left(-3\right)k5k=-30000\)
\(\Rightarrow\left(-30\right).k^3=-30000\)
\(\Rightarrow k^3=1000\)
\(\Rightarrow k=10\)
\(\Rightarrow x=20;y=-30;z=50\)
Vậy bộ số \(\left(x;y;z\right)\) là \(\left(20;-30;50\right)\)
Câu 3:
Giải:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{3b}=\frac{b}{3c}=\frac{c}{3d}=\frac{d}{3a}=\frac{a+b+c+d}{3b+3c+3d+3a}=\frac{a+b+c+d}{3\left(a+b+c+d\right)}=\frac{1}{3}\)
\(\frac{a}{3b}=\frac{1}{3}\Rightarrow3a=3b\Rightarrow a=b\)
Tương tự ta có b = c, c = d, d = a
\(\Rightarrow a=b=c=d\)
\(\Rightarrowđpcm\)
3, áp dụng tính chất dãy tỉ số bằng nhau:
=>\(\frac{a}{3.b}\)=\(\frac{b}{3.c}\)=\(\frac{c}{3.d}\) =\(\frac{d}{3.a}\) =\(\frac{a+b+c+d}{3\left(b+c+a+d\right)}\) =\(\frac{1}{3}\)
\(\Rightarrow\)\(\frac{a}{3b}\)=\(\frac{1}{3}\) =>\(\frac{1.b}{3.b}\) =\(\frac{b}{3.b}\) =>\(\frac{a}{3b}\) =\(\frac{b}{3b}\) =>...a=b (1)
\(\frac{c}{3d}\)=\(\frac{1}{3}\) =>\(\frac{1.d}{3.d}\) =\(\frac{d}{3d}\) =>\(\frac{c}{3d}\) =\(\frac{d}{3d}\) =>...c=d (2)
\(\frac{b}{3c}\) =\(\frac{1}{3}\) =>\(\frac{1.c}{3.c}\) =\(\frac{c}{3c}\)=>\(\frac{b}{3c}\) =\(\frac{c}{3c}\)=>..b=c (3)
\(\frac{d}{3a}\)=\(\frac{1}{3}\) =>\(\frac{1.a}{3.a}\) =\(\frac{a}{3a}\)=>\(\frac{d}{3a}\) =\(\frac{a}{3a}\)...=>d=a (4)
từ (1).(2).(3)(4)=>a=b=c=d(dpcm)

a)\(A=12-\left|x-3\right|-\left|y+7\right|\)
\(-\left|x-3\right|\le0;-\left|y+7\right|\le0\)
\(\Rightarrow A\le12-0-0=12\)
Vậy Max A = 12 <=> x = 3 ; y = -7
b)\(B=-\left(x-2018\right)^6-1\)
\(-\left(x-2018\right)^6\le0\)
\(B\le0-1=-1\)
Vậy Max B = -1 <=> x = 2018
a) \(A=12-\left|x-3\right|-\left|y+7\right|\)
Nhận thấy: \(\left|x-3\right|\ge0;\)\(\left|y+7\right|\ge0\)
suy ra: \(A=12-\left|x-3\right|-\left|y+7\right|\le12\)
Vậy MIN A = 12
Dấu "=" xảy ra <=> \(x=3;y=-7\)
b) \(B=-\left(x-2018\right)^6-1\)
Nhận thấy: \(\left(x-2018\right)^6\ge0\)
suy ra: \(B=-\left(x-2018\right)^2-1\le-1\)
Vậy MIN B = -1
Dấu "=" xảy ra <=> \(x=2018\)
c) \(C=\frac{20}{7}-\left|x+8\right|-\left(3y+7\right)^{2016}\)
Nhận thấy: \(\left|x+8\right|\ge0\) \(\left(3y+7\right)^{2016}\ge0\)
suy ra: \(C=\frac{20}{7}-\left|x+8\right|-\left(3y+7\right)^{2016}\le\frac{20}{7}\)
Vậy MIN C = 20/7
Dấu "=" xảy ra <=> \(x=-8;y=-\frac{7}{3}\)

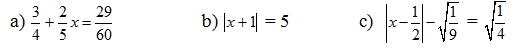
ờm cho tui xin cái đề i
bruh