Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cắt hai tam giác vuông bằng nhau từ một tấm bìa, chẳng hạn ta được hai hình sau:
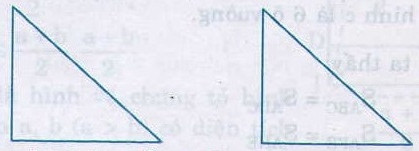
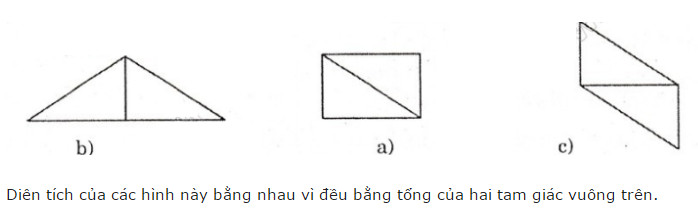
Ghép hai tam giác trên để tạo thành:

Bài 1:
Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
DO đó: F là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình
=>EF//BC
hay BEFC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BEFC là hình thang cân

b) Giả sử MNPQ là hình chữ nhật
=> ^QMN=90do HAY QM vuong goc voi MN
Lai co MN//BC
=> BC vuong goc voi QM
Ma QM //AO
=> AO vuong goc voi BC
=> O thuoc duong cao ke tu A den BC
Goi giao diem cua AO VA BC LA H
Để SMNPQ=SABC
=> MQ.QP=(BC.AH)/2
Mà QP=BC/2
=> MQ=AH
Ma MQ=AH/2
=> AH=AO/2
Mà AO hay AH vuong goc voi BC
=> BC la trung truc cua AO .
Vay de tu giac MNPQ vua la HCN vua co dien h =tam giac ABC thi BC phai la trung truc cua AO
a,Do tia AO nằm giữa tia AB và tia AC(gt)
Gọi O là điểm nằm giữa đoạn thẳng BC
sao cho BO< OC
M,N,P,Q lần lượt là trung điểm của OB,OC,AC,AB (gt)
=>BM=MO;ON=NC;CP=PA;AQ=QB
Vậy ta có:PQ là đường trung bình của tam giác ABC nên PQ//=1/2 BC (1)
Tương tự:
PN là đường trung bình của tam giác ACO nên PN//=1/2 AO (2)
QM là đường trung bình của tam giác ABO nên QM//=1/2 AO (3)
Từ (2),(3) suy ra:
PN//=QM=1/2 OA ( t/c 2 đường thẳng//) (4)
Do đó PQ//=MN
=> Tứ giác MNPQ là hình bình hành
b,theo cmt : PN//=QM=1/2 OA
Mặt khác, AO là cạnh đối diện của 2 góc B và góc C
Từ đó=>góc B=góc C
=> tam giác ABC cân tại A
=>O là trung điểm của BC
=>AO _|_BC nên góc AOB=góc AOC=90°
=> 3 điểm B,O,C thẳng hàng (vì BOC=180°=góc AOB+góc AOC)
M,N là trung điểm của OB và OC(gt)
nên B,M,O,N,C thẳng hàng.
=>QM_|_BC và PN_|_BC
Hay góc QMN=góc PNM=1 vuông (5)
Theo (1) PQ//BC
=>PQ_|_QM ; PQ_|_PN
Hay góc MQP=góc NPQ=1 vuông (6)
Từ (5),(6) suy ra:
Tứ giác MNPQ là hình chữ nhật (đpcm)

Xét \(\Delta\)ABC có: D là trung điểm của AB
M là trung điểm của BC
\(\Rightarrow\)DM là đường trung bình của \(\Delta ABC\)
\(\Rightarrow DM\)//AC hay DM//AE
Ta có : M là trung điểm của BC
E là trung điểm của CA
\(\Rightarrow\)ME là đường trung bình của \(\Delta\)ABC
\(\Rightarrow\)ME//AB hay ME//AD
Xét tứ giác ADME có: DM//AE(cmt)
ME//AD(cmt)
\(\Rightarrow\)ADME là hình bình hành
Nếu \(\Delta\)ABC cân tại A có đường trung tuyến AM
\(\Rightarrow\)AM đồng thời là tia phân giác của \(\widehat{A}\)
Xét hình bình hành ADME có đường chéo AM là tia phân giác của \(\widehat{A}\)(cmt)
\(\Rightarrow\)ADME là hình thoi
Nếu \(\Delta\)ABC vuông tại A
\(\Rightarrow\widehat{A}=90^0\)
Xét hình bình hành ADME có \(\widehat{A}=90^0\)(cmt)
\(\Rightarrow\)ADME là hình chữ nhật
d/ Xét \(\Delta ABC\) vuông tại A, đường trung tuyến AM
\(\Rightarrow AM=\frac{1}{2}BC\)(Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng 1/2 cạnh huyền)
Áp dụng định lí Py-ta-go vào tam giác ABC vuông tại A ta có:
BC2=AB2+AC2
\(\Leftrightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Leftrightarrow BC=\sqrt{6^2+8^2}\)
\(\Leftrightarrow BC=10\left(cm\right)\)
Khi đó:AM=\(\frac{1}{2}.BC=\frac{1}{2}.10=5\left(cm\right)\)
Vậy trong trường hợp tam giác ABC vuông tại A, AB=6cm và AC=8cm thì AM=5cm
Ta ghép như sau:
Diện tích 3 hình này đều bằng nhau vì cùng bằng tổng diện tích của hai tam giác vuông ban đầu.