Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi bán kính hình trụ là x > 0.
Khi đó ta có diện tích của hai đáy thùng là S 1 = 2 πx 2 Diện tích xung quanh của thùng là S 2 = 2 πxh = 2 πx V πx 2 = 2 V x
trong đó h là chiều cao của thùng và từ V = πx 2 . h ⇒ h = V πx 2
Vậy diện tích toàn phần của thùng là S = S 1 + S 2 = 2 πx 2 + 2 V x
Để tiết kiệm vật liệu nhất thì S phải bé nhất. Áp dụng bất đẳng thức AM-GM ta có
S = 2 πx 2 + V 2 x + V 2 x ≥ 2 . 3 πV 2 4 3
Do đó S bé nhất khi và chỉ khi πx 2 = V 2 x ⇔ x = V 2 π 3
Đáp án A
Chọn đáp án A.
Gọi r, h lần lượt là bán kính đáy và chiều cao của lon sữa bò cần thiết kế.
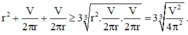
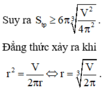
Đáp án D.
Khối nón cụt có thể tích là V = πh 3 R 2 + R . r + r 2 mà h = 3 V = π ⇒ R 2 + R . r + r 2 = 1 (*).
Ta có P = R + 2 r ⇔ R = P - 2 r thay vào (*), ta được P - 2 r 2 + P - 2 r r + r 2 = 1
⇔ P 2 - 4 P r + 4 r 2 + P r - 2 r 2 + r 2 - 1 = 0 ⇔ 3 r 2 - 3 P r + P 2 - 1 = 0 (I).
Vậy phương trình (I) có nghiệm khi và chỉ khi ∆ I = - 3 P 2 - 4 . 3 . P 2 - 1 ≥ 0 ⇔ P ≤ 2 .
Vậy giá trị lớn nhất của P là 2.
Đáp án B
Phương pháp giải: Chuẩn hóa thể tích, đưa diện tích toàn phần về hàm số, khảo sát hàm (hoặc bất đẳng thức) tìm min
Lời giải:
Thể tích của khối trụ là 
Chuẩn hóa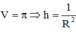 
Diện tích toàn phần của hình trụ là 
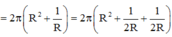
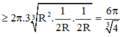
Dấu bằng xảy ra khi và chỉ khi 
Ta có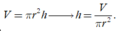 
Gọi t là giá tiền của một đơn vị diện tích vật liệu để làm mặt xung quanh, suy ra giá tiền của một đơn vị diện tích vật liệu để làm mặt đáy là 3t
Diện tích mặt xung quanh 
giá tiền mặt xung quanh là 
Diện tích hai mặt đáy 
giá tiền hai mặt đáy là 
Tổng tiền hoàn thành sản phẩm:
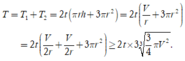
Dấu "=" xảy ra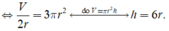 
Chọn C.
Đáp án D
Ta có V t = V = l . π R 2 ⇒ l = V π R 2
S t = l .2 π R + 2 π R 2 ⇒ S t = V π R 2 π R + 2 π R 2 = 2 ( π R 2 + V R )
S t = 2 ( π R 2 + V 2 R + V 2 R ) ≥ 2.3 π R 2 . V 2 R . V 2 R 3 = 6 π V 2 4 3
Dấu “=” xảy ra khi và chỉ khi π R 2 = V 2 R ⇔ R = V 2 π 3
Ta có:
Diện tích vật liệu để làm vỏ hộp là:
Ta có:
Bảng biến thiên:
Vậy, để tiết kiệm vật liệu nhất thì bán kính đáy phải bằng V 2 π 3 .
Chọn A.