Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bán kính của các hạt nhân chuyển động trong từ trường có biểu thức
\(R=\frac{mv}{qB}\)
=> \(R_{\alpha}=\frac{m_{\alpha}v_0}{q_{\alpha}B}=\frac{4.v_0}{2.q_e.B}=\frac{2v_0}{q_eB}.\left(1\right)\)
\(R_p=\frac{m_pv_0}{q_pB}=\frac{1.v_0}{q_e.B}=\frac{v_0}{q_eB}.\left(2\right)\)
\(R_T=\frac{m_Tv_0}{q_TB}=\frac{3.v_0}{q_e.B}=\frac{3v_0}{q_eB}.\left(3\right)\)
trong đó q là điện tích của hạt nhân = Z.q(e)
m là khối lượng hạt nhân = A(u)
Như vậy \(R_T>R_{\alpha}>R_T\)

1 B 0 B B 3 2 120
\(B_1 = B_0 \cos \omega t \)
\(B_2 = B_0 \cos (\omega t - \frac{2\pi}{3} )\)
\(B_3 = B_0 \cos (\omega t + \frac{2\pi}{3} )\)
Giả sử tại t = 0 thì \(B_1 = B_0; B_2 = \frac{B_0}{2} = B_3\)
Tổng hợp 3 véc tơ như hình vẽ \(\overrightarrow {B} = \overrightarrow {B_1} + \overrightarrow {B_2} +\overrightarrow {B_3} \) => \(B = \frac{B_0}{2} + B_0 = 1,5B_0.\)
Véc tơ cảm ứng từ tổng hợp cũng dao động với tần số \(\omega = \omega_0\).
Chọn đáp án.A.

T=2pi/4pi=0.5(s) => f=2 sau 5 s nó trở lại trạng thái ban đầu x=4cos(0)=4 vật ở biên
T=1(s)tại t=T/6 . ban đầu t=0 vật ở vtcb sau T/6 vật ở vị trí x=(a căn 3)/2 vì cos dương => -sin <0 => vật đi theo chiều âm . áp dụng ptđộc lâp tg cho v và a tìm nốt dc a

Bài 3:
Lại đạo hàm :<
Have: \(\left(\frac{x}{v}\right)'=\frac{x'v-v'x}{v^2}\)
Have also: \(\left\{{}\begin{matrix}v=x'\\v'=a=-\omega^2x\end{matrix}\right.\)
\(\Rightarrow\left(\frac{x}{v}\right)'=\frac{v^2+\omega^2x^2}{v^2}=1+\frac{x^2}{\frac{v^2}{\omega^2}}=1+\frac{x^2}{A^2-x^2}\)
Đạo hàm 2 vế theo thời gian biểu thức: \(\frac{x_1}{v_1}+\frac{x_2}{v_2}=\frac{x_3}{v_3}\) :
\(\left(1+\frac{x_1^2}{A_1^2-x_1^2}\right)+\left(1+\frac{x_2^2}{A_2^2-x_2^2}\right)=1+\frac{x_3^2}{A_3^2-x_3^2}\)
\(\Rightarrow1+\frac{x_1^2}{A_1^2-x_1^2}+\frac{x_2^2}{A_2^2-x_2^2}=\frac{x_3^2}{A_3^2-x_3^2}\Rightarrow\left|x_3\right|=3,4\left(cm\right)\)
Bài 2:
\(Cauchy:A_1+A_2\ge2\sqrt{A_1A_2}\Leftrightarrow10\ge2\sqrt{A_1A_2}\Rightarrow A_1A_2\le25\)
Have: \(A_1A_2=\sqrt{x_1^2+\frac{v_1^2}{\omega^2}}.\sqrt{x_2^2+\frac{v_2^2}{\omega^2}}=\sqrt{\left(x_1^2+\frac{v_1^2}{\omega^2}\right)\left(x_2^2+\frac{v_2^2}{\omega^2}\right)}\)
\(Bunhiacopxki:\left(a_1^2+a_2^2\right)\left(b_1^2+b_2^2\right)\ge\left(a_1b_1+a_2b_2\right)^2\)
\(\Rightarrow\left(x_1^2+\frac{v_1^2}{\omega^2}\right)\left(x_2^2+\frac{v_2^2}{\omega^2}\right)\ge\left(x_1.\frac{v_2}{\omega}+x_2.\frac{v_1}{\omega}\right)^2\)
\(\Rightarrow A_1A_2\ge\left(x_1.\frac{v_2}{\omega}+x_2\frac{v_1}{\omega}\right)\Leftrightarrow25\ge\left(\frac{x_1.v_2+x_2v_1}{\omega}\right)\)
\(\Leftrightarrow x_1v_2+x_2v_1\le25\omega\Leftrightarrow9\le25\omega\)
\(\Rightarrow\omega\ge\frac{9}{25}=0,36\left(rad/s\right)\)
This exercise is hardest :<

+ Vì M, N chuyển động tròn đều nên K cũng chuyển động tròn đều với cùng tốc độ dài là v = ω . R = 1 m/s.
+ Mặc khác: tốc độ trung bình trong 1 chu kỳ được tính: v t b = 4 R T = 4 R ω 2 π = 4. v 2 π = 2 v π = 0 , 63 m/s » 61,5 cm/s.
Đáp án C
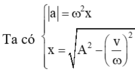
Chọn đáp án C.
Ta có: v = ω r , a h t = v 2 r