Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn ơi Hình chũ nhật không có đường chéo
Chỉ có hình thoi mới có đường chéo thôi
HỌC TỐT !


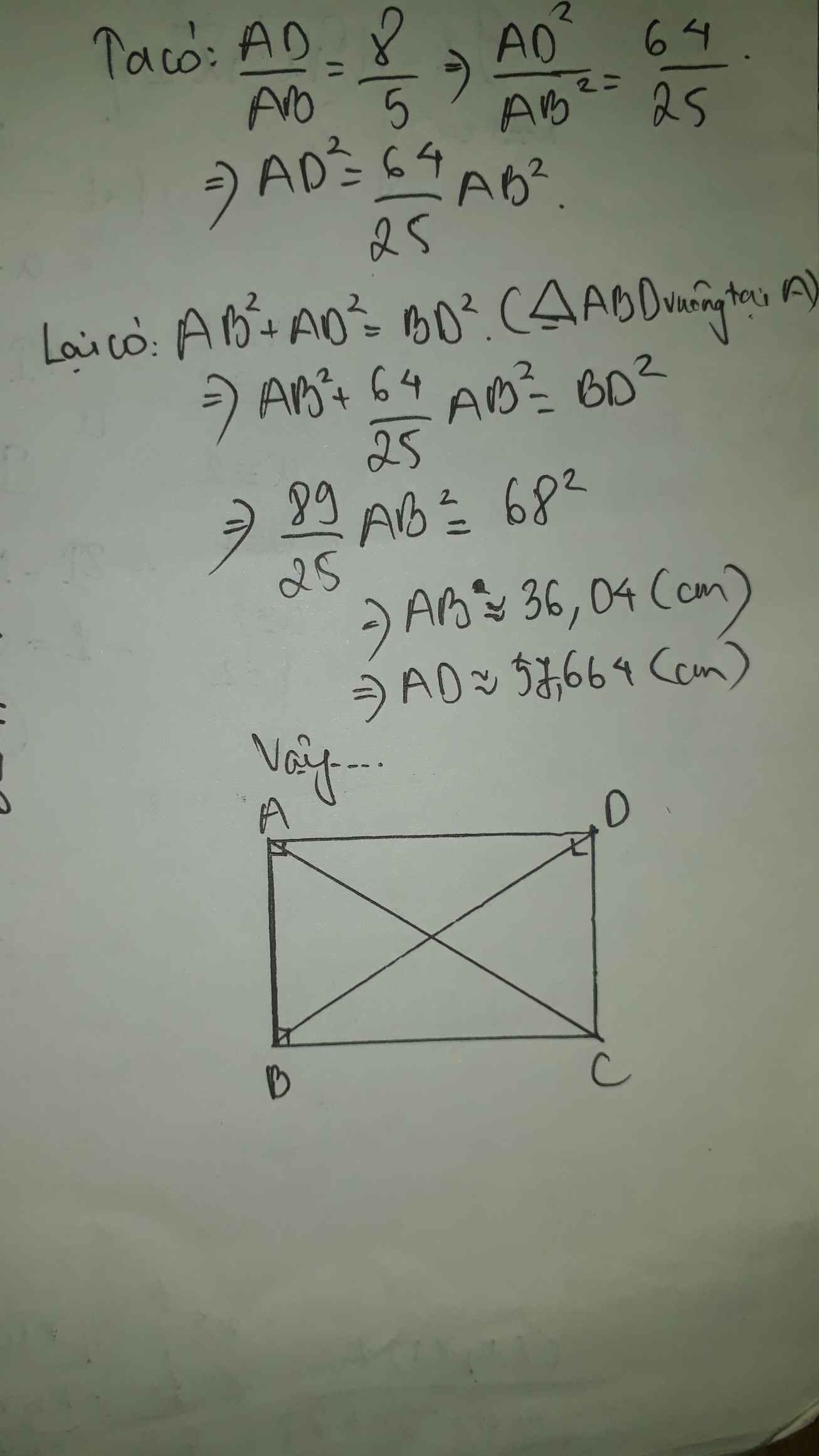
Ta có: \(\dfrac{AD}{AB}=\dfrac{8}{15}\)
nên \(AD=\dfrac{8}{15}AB\)
Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AD^2+AB^2\)
\(\Leftrightarrow\left(\dfrac{8}{15}AB\right)^2+AB^2=68^2=4624\)
\(\Leftrightarrow AB^2\cdot\dfrac{289}{225}=4624\)
\(\Leftrightarrow AB^2=3600\)
\(\Leftrightarrow AB=60\left(cm\right)\)
\(\Leftrightarrow AD=\dfrac{8}{15}AB=\dfrac{8}{15}\cdot60=32\left(cm\right)\)
\(\Leftrightarrow CD=60cm;BC=32cm\)

Bài 1:
Theo đề, ta có: \(\dfrac{AB}{BC}=\dfrac{30}{7}:\dfrac{40}{7}=\dfrac{3}{4}\) và \(AC=4+5+\dfrac{2}{7}+\dfrac{5}{7}=10\)
=>AB/3=BC/4
Đặt AB/3=BC/4=k
=>AB=3k; BC=4k
Xét ΔABC vuông tại B có \(AC^2=AB^2+BC^2\)
\(\Leftrightarrow25k^2=100\)
=>k=2
=>AB=CD=6(cm); BC=AD=8(cm)

Gọi chiều dài của hcn là a, chiều rộng của hcn là b
(cm; a>b>0)
Ta có: a2 + b2 = 292 (Pytago)
<=> a2 + b2 = 841
TH1: a = 20
<=> 202 + b2 = 841
<=> b = 21 (loại)
TH2: b = 20
<=> a2 + 202 = 841
<=> a = 21 (t/m)
=> Chiều dài hcn là 21cm, chiều rộng hcn là 20cm

Hình chữ nhật ABCD có AB = 3cm, BC = 3 cm nên
Vậy ∠ (BAC) = 30 °
∠ (DAC) = 90 ° - 30 ° = 60 °