
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

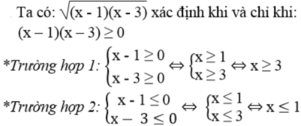

tìm x để bt xác định
cho mỗi biểu thức trong căn
lớn hơn hoặc =0

a)\(\sqrt{\left(x-1\right)\left(x-3\right)}\ge0\)
\(\Rightarrow\left(x-1\right)\left(x-3\right)\ge0\)
\(\Rightarrow1\le x\le3\)
b)\(\sqrt{x^2-4}\)
\(=\sqrt{x^2-2^2}=\sqrt{\left(x-2\right)\left(x+2\right)}\)
\(\Rightarrow\left(x-2\right)\left(x+2\right)\ge0\)
\(\Rightarrow-2\le x\le2\)
c)\(\sqrt{\frac{x-2}{x+3}}=\frac{\sqrt{x-2}}{\sqrt{x+3}}\)
\(\Rightarrow\sqrt{x-2}\ge0\)
\(\Rightarrow x\ge2\)
\(\Rightarrow\sqrt{x+3}>0\)
\(\Rightarrow x+3>0\Leftrightarrow x>-3\)
\(\Rightarrow x\in\left(-\infty;-3\right)\)U[\(2;\infty\))
d)\(\sqrt{\frac{2+x}{5-x}}=\frac{\sqrt{2+x}}{\sqrt{5-x}}\)
\(\Rightarrow\sqrt{2+x}\ge0\)
\(\Rightarrow2+x\ge0\)
\(\Rightarrow x\ge-2\)
\(\Rightarrow\sqrt{5-x}>0\)
\(\Rightarrow5-x>0\Leftrightarrow x>5\)
\(\Rightarrow x\in\)[-2;5)
a) ĐKXĐ : \(\left(x-1\right)\left(x-3\right)\ge0\Leftrightarrow\begin{cases}x-1\ge0\\x-3\ge0\end{cases}\)hoặc \(\begin{cases}x-1\le0\\x-3\le0\end{cases}\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x\ge3\\x\le1\end{array}\right.\)
b) \(x^2-4\ge0\Leftrightarrow x^2\ge4\Leftrightarrow\left|x\right|\ge2\Leftrightarrow\left[\begin{array}{nghiempt}x\ge2\\x\le-2\end{array}\right.\)
c) \(\frac{x-2}{x+3}\ge0\Leftrightarrow\begin{cases}x-2\ge0\\x+3>0\end{cases}\) hoặc \(\begin{cases}x-2\le0\\x+3< 0\end{cases}\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x\ge2\\x< -3\end{array}\right.\)
d) \(\frac{2+x}{5-x}\ge0\) \(\Leftrightarrow\begin{cases}2+x\ge0\\5-x>0\end{cases}\) hoặc \(\begin{cases}2+x\le0\\5-x< 0\end{cases}\)
\(\Leftrightarrow-2\le x< 5\)

bạn nhi nguyễn "T ích sai cho mình " chứng tỏ bạn rất oc cko :))

a, Để \(\sqrt{\left(x-1\right)\left(x-3\right)}\) xác định thì (x-1)(x-3)\(\ge\)0
TH1: \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x\ge3\end{matrix}\right.\Leftrightarrow}x\ge3}\)TH2:\(\left\{{}\begin{matrix}x-1\le0\\x-3\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le1\\x\le3\end{matrix}\right.\Leftrightarrow}x\le1}\) Vậy nếu \(x\ge3\) hoặc \(x\le1\) thì biểu thức có nghĩa
b, Để \(\sqrt{x^2-4}=\sqrt{\left(x-2\right)\left(x+2\right)}\)có nghĩa thì (x-2)(x+2)\(\ge0\)
TH1: \(\left\{{}\begin{matrix}x-2\ge0\\x+2\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge2\\x\ge-2\end{matrix}\right.\Leftrightarrow x\ge}2}\)TH2:\(\left\{{}\begin{matrix}x-2\le0\\x+2\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le2\\x\le-2\end{matrix}\right.\Leftrightarrow}x\le-2}\)Vậy nếu \(x\ge2\) hoặc \(x\le-2\) thì biểu thức có nghĩa

1) a) Căn thức có nghĩa \(\Leftrightarrow4-2x\ge0\Leftrightarrow2x\le4\Leftrightarrow x\le2\)
b) Thay x = 2 vào biểu thức A, ta được: \(A=\sqrt{4-2.2}=\sqrt{0}=0\)
Thay x = 0 vào biểu thức A, ta được: \(A=\sqrt{4-2.0}=\sqrt{4}=2\)
Thay x = 1 vào biểu thức A, ta được: \(A=\sqrt{4-2.1}=\sqrt{2}\)
Thay x = -6 vào biểu thức A, ta được: \(A=\sqrt{4-2.\left(-6\right)}=\sqrt{16}=4\)
Thay x = -10 vào biểu thức A, ta được: \(A=\sqrt{4-2.\left(-10\right)}=\sqrt{24}=2\sqrt{6}\)
c) \(A=0\Leftrightarrow\sqrt{4-2x}=0\Leftrightarrow4-2x=0\Leftrightarrow x=2\)
\(A=5\Leftrightarrow\sqrt{4-2x}=5\Leftrightarrow4-2x=25\Leftrightarrow x=\frac{-21}{2}\)
\(A=10\Leftrightarrow\sqrt{4-2x}=10\Leftrightarrow4-2x=100\Leftrightarrow x=-48\)

\(a,\)\(\sqrt{5x^2-3x-8}\)
\(đkxđ\Leftrightarrow5x^2-3x-8\ge0\)
\(\Rightarrow5x^2+5x-8x-8\ge0\)
\(\Rightarrow5x\left(x+1\right)-8\left(x+1\right)\ge0\)
\(\Rightarrow\left(x+1\right)\left(5x-8\right)\ge0\)
\(\Rightarrow\orbr{\begin{cases}x+1\ge0;5x-8\ge0\\x+1< 0;5x-8< 0\end{cases}\Rightarrow\orbr{\begin{cases}x\ge-1;x\ge\frac{8}{5}\\x< -1;x< \frac{8}{5}\end{cases}\Rightarrow}\orbr{\begin{cases}x\ge\frac{8}{5}\\x< -1\end{cases}}}\)
\(b,\)\(\sqrt{5x^2+4x+7}\)
\(đkxđ\Leftrightarrow5x^2+4x+7\ge0\)
\(\Rightarrow5\left(x^2+\frac{4}{5}x+\frac{7}{5}\right)\ge0\)
\(\Rightarrow5\left(x^2+2.\frac{2}{5}+\frac{4}{25}-\frac{4}{25}+\frac{7}{5}\right)\ge0\)
\(\Rightarrow5\left[\left(x+\frac{2}{5}\right)^2+\frac{31}{25}\right]\ge0\)
\(\Rightarrow5\left(x+\frac{2}{5}\right)^2+\frac{31}{5}\ge0\)( luôn đúng )
\(\Rightarrow\)Biểu thức được xác định với \(\forall x\)

mọi ng ơi mk viết thiếu dấu ngoặc nha.thiếu ngoặc lownns nha. đóng ngoắc ở trước dấu chia