Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

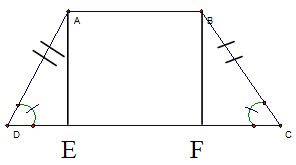
ABCD (AB // DC) LÀ Hình thang cân ta có :
\(\widehat{D}=\widehat{C};AD=BC\)
Xét Δ AED và Δ BFC ta có :
\(\widehat{AED}=\widehat{BFC}=90^o\)
\(\widehat{C}=\widehat{D}=\left(cmt\right)\)
\(AD=BC\left(cmt\right)\)
= > Δ AED = Δ BFC (cạnh huyền – góc nhọn)
= > DE = CF

A B D E F C
Vì ABCD là hình thang cân ( gt)
\(\Rightarrow\left\{{}\begin{matrix}AB=DC\\\widehat{B}=\widehat{C}\end{matrix}\right.\)
Xét \(\Delta AED\) và \(\Delta BFC\) có:
\(\widehat{E}=\widehat{F}=90^0\)
AD = BC
\(\widehat{C}=\widehat{D}\)
=> tam giác AED = tam giác BFC ( ch- gn)
=> DE =CF

Giải:
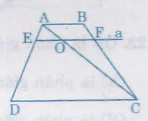
a) Nối AC cắt EF tại O
∆ADC có EO // DC => AEEDAEED = AOOCAOOC (1)
∆ABC có OF // AB => AOOCAOOC = BFFCBFFC (2)
Từ 1 và 2 => AEEDAEED = BFFCBFFC
b) Từ AEEDAEED = BFFCBFFC => AEED+AEAEED+AE= BFFC+BFBFFC+BF
hay AEADAEAD=BFBCBFBC
c) Từ AEEDAEED = BFFCBFFC => AE+EDEDAE+EDED= BF+FCFCBF+FCFC
=> AD

Vì hình thang ABCD cân
AD = BC;
Ĉ = D̂
Xét hai tam giác vuông AED và BFC có:
AD = BC
Ĉ = D̂
⇒ ΔAED = ΔBFC (cạnh huyền – góc nhọn)
⇒ DE = CF.

Sai đề rồi bn nhé :\(\widehat{A}+\widehat{D}=\widehat{B}+\widehat{C}\)
Vì AB//CD \(\Rightarrow\widehat{A}+\widehat{D}=180\) ;\(\widehat{B}+\widehat{C}=180\)
=>đpcm

a, Do I là trung điểm của DC
suy ra: IC=1/2DC
Mà AB=1/2DC nên AB=CI(*)
Ta có: AB//CD
MÀ I nằm trên cạnh DC
suy ra AB//IC(**)
Từ (*);(**) suy ra tứ giác ABCI là hình bình hành
b, Chứng minh tương tự ta cũng có tứ giác ABID là hình bình hành.
c, Chứng minh tam giác bằng nhau suy ra IA=IC còn cách còn lại bạn tự làm nha dễ đấy
bạn làm hộ mik lốt câu c đi.Mik chứng minh đc IA=IC rồi nhưng không biết làm gì nữa

Vì AB // CD nên \(\hept{\begin{cases}\widehat{A}+\widehat{D}=180^0\\\widehat{B}+\widehat{C}=180^0\end{cases}}\)(định lí hình thang)
Mà \(\widehat{A}=5\widehat{D}\)=> \(\widehat{5D}+\widehat{D}=180^0\)=> \(6\widehat{D}=180^0\)=> \(\widehat{D}=30^0\)(1)
Thay (1) vào \(\widehat{A}=5\widehat{D}\)ta có :
\(\widehat{A}=5\cdot30^0=150^0\)
Lại có : \(\widehat{B}=4\widehat{C}\)
=> \(4\widehat{C}+\widehat{C}=180^0\)
=> \(5\widehat{C}=180^0\)
=> \(\widehat{C}=36^0\)(2)
Thay (2) vào \(\widehat{B}=4\widehat{C}\)ta có :
=> \(\widehat{B}=4\cdot36^0=144^0\)
Vậy : ^A = 1500 , ^B = 1440 , ^C = 360 , ^D = 300

giup mik pls
cần hình vẽ không bạn