Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chọn gốc tọa độ tại A, chiều dương từ A đến B, gốc thời gian lúc 7h
x1 = x0(1) +v1t1
=0+50t
=50t
x2 = x0(2) +v2t2
=100 - 40t
Hai xe gặp nhau lúc:
50t= 100 - 40t
-90t= - 100
t=1 ( xấp xỉ) ( giờ)
Vậy 2 xe gặp nhau sau 1h lúc 8h
Vị trí của 2 xe khi gặp nhau cách A là
s=v.t =50.1=50 (km)
b)
bạn tự vẽ nhé
c) ptcđ: x3 = x0(3) + v3t3
=10+20t
Hai xe gặp nhau lúc:
10+20t = 50t
30t=10
t=10/30
t=20 phút (xấp xỉ)= 1/3 h
Vậy 2 xe gặp nhau sau 20 phút lúc 9h20
vị trí 2 xe gặp nhau cách A là
s= vt =50. 1/3= 16,7 (km) (xấp xỉ)
Theo mình xe 1 và xe 3 không thể gặp nhau vì
1: là xe 1 khởi hành lúc 7h xe 2 chạy trễ hơn mà còn chạy
xe 2 lúc 9h với tốc độ chậm hơn nên
2: là xe 1 chạy vs vận tốc 50km/h 2 xe không thể gặp nhau
xe 2 là 20km/h
1 và 2 => 2 xe không thể gặp nhau
Mình trả lời lại cho câu trả lời của bạn Đông. Mong thầy cô và các bạn cho ý kiến.
a) ta có ptcđ: x = x0 + v(t-t0)
Theo dữ kiện của đề bài. Ta có xA= 50(t-7) (các bạn có thể để xA = 50t. Nếu để như này thì t là khoảng thời gian xe chạy không phải thời điểm). Và xB=100-40(t-7).
Hai xe gặp nhau thì xA=xB <=> 50(t-7) = 100-40(t-7) (Giải phương trình) => t= 73/9 giờ. (hay 8h 6,67 phút. Chúng ta để phân số để tính chứ không làm tròn như bài giải của Đông để có kq chính xác.)
Vị trí hai xe gặp nhau x=55,55km.
b) Vị trí hai xe cách nhau 20km. Ta có (trị tuyệt đối) /xA-xB/=20.
Tức là trường hợp 2 xe chưa tới nhau còn cách nhau 20km. và hai xe đã đi qua nhau và cách nhau 20km. Đến đây giải pt toán học trên là ra. kết quả t=1,3h và t=8/9h.
c). Câu này mới là câu thắc mắc.
Xét lúc 9h Xe C mới bắt đầu xuất phát thì xe A đã đi được 2 tiếng (100km) cách C đến 90km.
Vậy với vận tốc 20km/h xuất phát sau 90km so với xe A vận tốc 50km/h thì C không thể nào đuổi kịp A (hay nói cách khác hai xe không gặp nhau.) Nhưng A có đi qua C.
cụ thể 9h xe C mới xuất phát trong khi xe A đi từ 7h. Tức là:
xA = 50(t-7)=10km thì gặp C. <=> t=7,2h hay 7h12 phút thì A qua C hay A và C gặp nhau. Vậy thầy cô và các bạn cho em hỏi. Nếu đề trắc nghiệm cho 4 kết quả trong đó có Vô nghiệm Và kết quả 7h12 phút thì chọn đáp án nào? Em xin cảm ơn.

a) Chọn Ox có gốc tại A, chiều dương hướng từ A sang B. Gốc thời gian là lúc hai xe bắt đầu chuyển động. Suy ra x 01 = 0; x 02 = 300 m.
- Với xe thứ nhất chuyển động theo chiều dương của Ox nên: v 01 = 10m/s và chuyển động nhanh dần đều nên a 1 = 2 m/ s 2 (do v 01 a 1 > 0) (0,25đ)
- Xe thứ hai chuyển động theo chiều âm của Ox nên v 02 = - 20 m/s và chuyển động chậm dần đều nên a 2 = 2 m/ s 2 (do v 02 a 2 < 0), x 2 = 300 m. (0,25đ)
Phương trình chuyển động của xe thứ nhất:
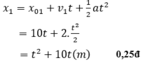
Phương trình chuyển động của xe thứ hai:
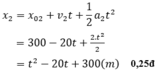
b) Khoảng cách giữa hai xe:
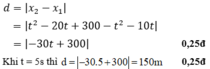
c) Hai xe gặp nhau khi: 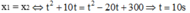 (0,25đ)
(0,25đ)
Vậy hai xe gặp nhau sau 10s.
Khi đó thay t = 10s vào ta có: 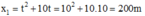 (0,25đ)
(0,25đ)
Suy ra vị trí gặp nhau cách vị trí xuất phát ban đầu của xe thứ 1 là 200 m.

< A B O x 1250
Đổi:
\(v_1=54km/h=15m/s\)
\(v_2=18km/h=5m/s\)
\(S=1,25km=1250m\)
Chọn trục toạ độ như hình vẽ.
Chọn mốc thời gian lúc 6h.
a) Phương trình chuyển động của xe A:
\(x_1=x_0+v.t\)
Có \(x_0=1250\); \(v=-15m/s\) (vì chuyển động ngược chiều dương của trục toạ độ)
\(\Rightarrow x_1=1250-15.t(m)\)
Phương trình chuyển động của xe B:
\(x_2=x_0+v_0t+\dfrac{1}{2}at^2\)
Có: \(x_0=0\); \(v_0=5m/s\); \(a=0,2m/s^2\)
\(\Rightarrow x_2=5.t+0,1.t^2(m)\)
b) Hai xe gặp nhau khi:
\(x_1=x_2\)
\(\Rightarrow 1250-15t=5t+0,1t^2\)
\(\Rightarrow 0,1t^2+20t-1250=0\)
Giải phương trình trên ta được \(t=50s\)
c) Quãng đường xe thứ 2 đi được là:
\(S_2=v_0t+\dfrac{1}{2}at^2=5.50+0,1.50^2=500(m)\)
d) Vận tốc xe thứ 2 là:
\(v_2=v_0+at=5+0,2.50=15(m/s)\)
e) Khi tắt máy, xe thứ 2 có vận tốc là: \(v_2=15(m/s)\)
Áp dụng công thức:
\(v^2-v_0^2=2aS\)
\(\Rightarrow a = \dfrac{v^2-v_0^2}{2S} = \dfrac{0^2-15^2}{2.150}=0,75(m/s^2)\)
Thời gian xe 2 đã đi là:
\(t_2=\dfrac{v_2}{a}=\dfrac{15}{0,75}=20s\)
Quãng đường xe thứ 1 đi được là: \(S_1=v_1.t_2=15.20=300m\)Khoảng cách hai xe khi xe 2 dừng lại là: \(150+300=450(m)\)

Gọi \(t\left(s\right)\)là thời gian để hai xe đuổi kịp nhau. \(\left(t>0\right)\)
Ta có: \(4t+\frac{1}{2}.0,2t^2=200+1.t+\frac{1}{2}.0,1.t^2\)
\(\Leftrightarrow\frac{1}{20}t^2+3t-200=0\)
\(\Leftrightarrow\orbr{\begin{cases}t=40\left(tm\right)\\t=-100\left(l\right)\end{cases}}\)
Vị trí hai xe gặp nhau cách A quãng đường là: \(4.40+\frac{1}{2}.0,2.40^2=320\left(m\right)\)

chọn hệ quy chiếu: gốc tọa độ trùng A
chiều dượng của Ox từ A đến B
gốc thời gian khi ô tô đi qua điểm A ( lúc 8h)
a) phương trình chuyển động của 2 xe
x1=10t - 0,1t^2
x2= 560 - 0,2t^2
2 xe gặp nhau <=> x1=x2
<=> t=40s
x=x1=x2= 240m
b) phương trình vận tốc của 2 xe: (v=v0 + at)
v1=10 - 0,2 .40 =2 m/s
v2= 0+ 0,4 .40 = 16 m/s
Chọn gốc thời gian là lúc 8h, gốc tọa độ tại A, chiều dương từ A đến B
ô tô 1: xo1 = 0; vo1 = 10m/s; a1 = -0,2m/s2
ô tô 2: xo1 = 560; vo1 = 0; a1 = 0,4m/s2
Giải
a) Phương trình chuyển động của hai xe:
x1 = x01 + v01t + 0,5a1t2 = 10t – 0,1t2 (1)
x2 = x02 + v02t + 0,5a2t2 = 560 – 0,2t2 (2)
b) Khi hai xe gặp nhau:
x1 = x2 => 10t – 0,1t2 = 560 – 0,2t2 => t = 40 s
=> x1 = x2 = 240 m.
c) Thời gian để xe một dừng lại:
v1 = vo1 + a1.t => t = 50 s;