Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Sử dụng công thức lãi kép kiểu 2 (gửi một số tiền đều đặn đầu hằng tháng):

Gọi M (đồng) là số tiền sinh viên đó gửi vào ngân hàng mỗi năm.
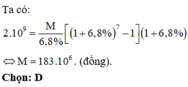

Chọn C
Gọi A là số tiền gửi ban đầu, n là số năm gửi.
Theo bài ra: Sau 1 năm, số tiền cả vốn lẫn lãi là : A + A. 8,4% =A. 1,084.
Sau 2 năm, số tiền cả vốn lẫn lãi là: A.1,084 + A. 1,084.8,4% = A. 1,084^2.
Sau n năm, số tiền cả vốn lẫn lãi là A. 1,084^n.
Số tiền này bằng 2 lần ban đầu nên: A. 1,084^n = 3A
ð n = ~ 14

Chọn A
Gọi T 0 là số tiền người đó gửi vào ngân hàng vào ngày 01/01 hàng năm, T n là tổng số tiền cả vốn lẫn lãi người đó có được ở cuối năm thứ n , với n ∈ ℕ * , r là lãi suất ngân hàng mỗi năm.
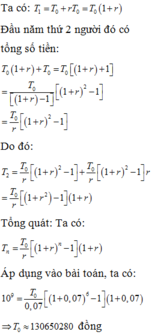

Đáp án D.
Số tiền gốc là lãi thu được khi gửi tiền vào tháng thứ 2 là:
2.000.000 1 + 0 , 55 % 59 + 200.000 1 + 0 , 55 % 59
Số tiền gốc là lãi thu được khi gửi tiền vào tháng thứ 2 là:
2.000.000 1 + 0 , 55 % 58 + 200.000 1 + 0 , 55 % 58
Số tiền gốc là lãi thu được khi gửi tiền vào tháng thứ 3 là:
2.000.000 1 + 0 , 55 % 57 + 200.000 1 + 0 , 55 % 57
…………………………………….
Số tiền gốc là lãi thu được khi gửi tiền vào tháng thứ 59 là
2.000.000 1 + 0 , 55 % 1 + 200.000 1 + 0 , 55 % 1
Do đó sau 5 năm (kể từ lần gửi đầu tiên) người đó nhận được tổng số tiền cả vốn lẫn lãi là
T = 200.000. 1 + 0 , 55 % .
1 − 1 + 0 , 55 % 60 1 − 1 + 0 , 55 % + 200.000 1 + 0 , 55 % 59
1 + 2 1 + 0 , 55 % − 1 + 3 1 + 0 , 55 − 2 + ...59 1 + 0 , 55 − 58
Mặt khác ta có:
x + x 2 + x 3 + ... + x n = x 1 − x n 1 − x = x − x n + 1 1 − x
Đạo hàm 2 vế ta có:
1 + 2 x + 3 x 2 + ... + n x n − 1 = 1 − n + 1 x n 1 − x + x − x n − 1 1 − x
Với x = 1 1 + 0 , 55 ; n = 59 ta có:
1 + 2 1 + 0 , 55 % − 1 + 3 1 + 0 , 55 − 2 + ....59 1 + 0 , 55 − 58 ≈ 1436
Vậy T = 539447312 đồng






Đáp án A
Gọi số tiền cần gửi vào mỗi năm là a đồng, ta có a 1 , 08 8 + a 1 , 08 7 + ... + a 1 , 08 1 = 2
⇔ 1 , 08 a 1 − 1 , 08 8 1 − 1 , 08 = 2 ⇔ a = 2 0 , 08 1 , 08 9 − 1 , 08 đồng.