Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

) Những cạnh song song với cạnh CC1 là: AA1, BB1, DD1
b) Những cạnh song song với cạnh A1D1 là: B1C1, BC, AD

a. Ta có: A1B1 // mp(ABCD)
A1B1 // mp(CDD1C1)
b. Ta có: AC // A1C1
Suy ra: AC không thuộc mp(A1B1C1)

Bài 1:
Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
DO đó: F là trung điểm của AC
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình
=>EF//BC
hay BEFC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BEFC là hình thang cân

A B C D O K a)Xét tứ giác OBKC, ta có:
OC//BK(BK//AC)
BO//KC(KC//BD)
=>tứ giác OBKC là hình bình hành
lại có:
AC \(\perp\) BD ( hai đường chéo)
BD//KC
=> \(\)góc OCK =90o
=> hình bình hành OBKC là hình chữ nhật
b)Ta có:
BC = OK ( do OCKD là hình chữ nhật)
AB=BC( cách cạnh hình thoi bằng nhau)
=> AB = OK
c)
* nếu tứ giác ABCD là hình vuông:
=>BD=AC
mà: BO=1/2BD
OC=1/2AC
=> BO = OC
=> hình chữ nhật OBKC là hình vuông.
Vậy HCN OBKC là hình vuông khi hình thoi ABCD là hình vuông

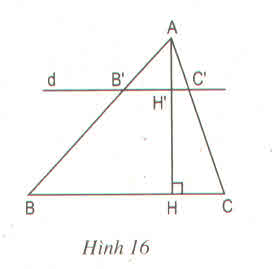
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = 1313 AH
B′C′BCB′C′BC = AH′AHAH′AH = 1313 => B'C' = 1313 BC
=> SAB’C’= 1212 AH'.B'C' = 1212.1313AH.1313
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = 1313 AH
B′C′BCB′C′BC = AH′AHAH′AH = 1313 => B'C' = 1313 BC
=> SAB’C’= 1212 AH'.B'C' = 1212.1313AH.1313BC
=>SAB’C’= (1212AH.BC)1919
mà SABC= 1212AH.BC = 67,5 cm2
Vậy SAB’C’= 1919.67,5= 7,5 cm2

Bài 1
a) Xét tam giác BCD có BM=MD(gt), BN=NC(gt) => MN là đg` TB => MN// DC => MN// DE(1)
và MN=1/2DC => MN= DE(2)
từ (1)và (2) => MNED là hbh
b) MNED là hbh(câu a) => MD//NE => ADM= DEN(đồng vị)
Xét tam giác ABD vg tại A có BM=DM=> AM là trung tuyến => AM=1/2BD= MD
=> tam giác ADM cân tại M => MDA = DAM
=> DEN= MAD (3)
MN//DE=> MN//AE => AMNE là hình thang (4)
từ (3)và (4) => AMNE là hình thang cân
c) để MNED là hình thoi \Leftrightarrow MNED là hbh có MD=DE \Leftrightarrow 1/2BD=1/2CD \Leftrightarrow BD = CD \Leftrightarrow tam giác BCD cân tại D \Leftrightarrow DBC=góc C \Leftrightarrow góc C=1/2góc B\Leftrightarrow góc C=2góc B
Vậy để MNED là hình thoi thì tam giác ABC có góc C=2góc B
- Bài 1
a) Xét tam giác BCD có BM=MD(gt), BN=NC(gt) => MN là đg` TB => MN// DC => MN// DE(1)
và MN=1/2DC => MN= DE(2)
từ (1)và (2) => MNED là hbh
b) MNED là hbh(câu a) => MD//NE => ADM= DEN(đồng vị)
Xét tam giác ABD vg tại A có BM=DM=> AM là trung tuyến => AM=1/2BD= MD
=> tam giác ADM cân tại M => MDA = DAM
=> DEN= MAD (3)
MN//DE=> MN//AE => AMNE là hình thang (4)
từ (3)và (4) => AMNE là hình thang cân
c) để MNED là hình thoi \Leftrightarrow MNED là hbh có MD=DE \Leftrightarrow 1/2BD=1/2CD \Leftrightarrow BD = CD \Leftrightarrow tam giác BCD cân tại D \Leftrightarrow DBC=góc C \Leftrightarrow góc C=1/2góc B\Leftrightarrow góc C=2góc B
Vậy để MNED là hình thoi thì tam giác ABC có góc C=2góc Bnhuquynhdat, 17 Tháng mười hai 2013#2 
nhuquynhdatGuest
bài 2
a) AB//CD => AB//CE(1)
Xét tam giác ADE có AH là đg` cao
lại có E đối xứng với D qua H => H là trung điểm của DE => AH là trung tuyến
=> tam giác ADE cân tại A
=> ADE=AED(goác đáy tam giác cân)
mặt khác ABCD là hình thang cân => ADC=góc C
=> góc C= AED
mà 2 góc này ở vị trí đồng vị của AE và BC => AE//BC(2)
từ (1)và (2) => ABCE là hbh
b) xét tam giác AHE và tam giác FHD có góc AHE=góc DHF(đối đỉnh)
DH=HE(gt)
AE//DF(gt)=> AEH=FDH(SLT)
=>tam giác AHE=tam giác FHD(gcg) => AH=HF => H là TĐ của AF
c) Ta có AH=HF(câu b)DH=HE(gt) => ADFE là hbh
mà AH vg góc với ED=> AF vg góc với ED => ADEF là hình thoi
lại có tam giác ADE cân tại A (câu a)=> AD=AE => ADEF là hình vg
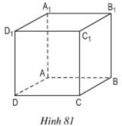
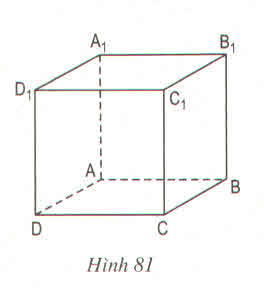

a) Những cạnh song song với cạnh CC1 là: AA1, BB1, DD1
b) Những cạnh song song với cạnh A1D1 là: B1C1, BC, AD