K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NN
1
1 tháng 4 2016
\((6^2)^x.6^3<2^x.2^7.\dfrac{(3^3)^x}{3}=(2.3^3)^x.\dfrac{2^7}{3}\Leftrightarrow \left(\dfrac{2.3^3}{6^2}\right)^x>\dfrac{3.6^3}{2^7}\)
Suy ra \(\left(\dfrac{3}{2}\right)^x>\left(\dfrac{3}{2}\right)^4\).
Vậy x>4
LN
27 tháng 8 2017
phá trị tuyệt đối của nó ra dc 2 th .1th chuyển vế rồi cho denta=0 là oke .1 th có 1 no vs mọi m rồi kết hợp kq thì ta dc gtri của m ở th 1 là no cần tìm thảo mãn cả 2 th đều ra 1 no
AH
Akai Haruma
Giáo viên
19 tháng 12 2017
Câu 1:
\(A=\int \frac{2\sin x+\cos x}{3\sin x+2\cos x}dx\)
\(A=\int \frac{\frac{8}{13}(3\sin x+2\cos x)-\frac{1}{13}(3\cos x-2\sin x)}{3\sin x+2\cos x}dx\)
\(A=\frac{8}{13}\int dx-\frac{1}{13}\int \frac{(3\cos x-2\sin x)dx}{3\sin x+2\cos x}\)
\(A=\frac{8}{13}x-\frac{1}{13}\int \frac{d(3\sin x+2\cos x)}{3\sin x+2\cos x}\)
\(A=\frac{8}{13}x-\frac{1}{13}\ln |3\sin x+2\cos x|+c\)
AH
Akai Haruma
Giáo viên
19 tháng 12 2017
Câu 2:
Ta có: \(I=\int \frac{x^3}{x^4+3x^2+2}dx=\int \frac{x^3}{(x^2+1)(x^2+2)}dx\)
\(=\int x^3\left(\frac{1}{x^2+1}-\frac{1}{x^2+2}\right)dx=\int \frac{x^3dx}{x^2+1}-\int \frac{x^3}{x^2+2}dx\)
\(=\frac{1}{2}\int \frac{x^2d(x^2+1)}{x^2+1}-\frac{1}{2}\int \frac{x^2d(x^2+2)}{x^2+2}\)
\(=\frac{1}{2}\int \left(1-\frac{1}{x^2+1}\right)d(x^2+1)-\frac{1}{2}\int \left(1-\frac{2}{x^2+2}\right)d(x^2+2)\)
\(=\frac{1}{2}\int d(x^2+1)-\frac{1}{2}\int \frac{d(x^2+1)}{x^2+1}-\frac{1}{2}\int d(x^2+2)+\int \frac{d(x^2+2)}{x^2+2}\)
\(=\frac{x^2+1}{2}-\frac{1}{2}\ln |x^2+1|-\frac{x^2+2}{2}+\ln |x^2+2|+c\)
\(=\ln |x^2+2|-\frac{1}{2}\ln |x^2+1|+c\)
Q
31 tháng 3 2017
Số nghiệm của các phương trình đã cho chính là số giao điểm của đồ thị hàm số y = f(x) ở vế trái của phương trình cới trục hoành ở câu a), b) và với đường thẳng y = -1 ở câu c).
a) Xét hàm số y = x3 – 3x2 + 5 . Tập xác định : R.
y' = 3x2 - 6x = 3x(x - 2); y' = 0 ⇔ x = 0,x = 2.
Bảng biến thiên:
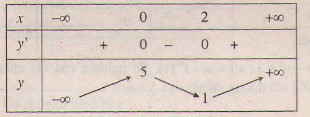
Đồ thị như hình bên.
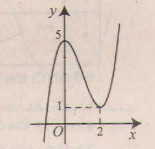
Từ đồ thị ta thấy phương trình đã cho có nghiệm duy nhất .
b) Xét hàm số y = -2x3 + 3x2 - 2 . Tập xác định : R.
y' = -6x2 + 6x = -6x(x - 1); y' = 0 ⇔ x = 0,x = 1.
Đồ thị như hình bên. Từ đồ thị ta thấy phương trình đã cho có nghiệm duy nhất .
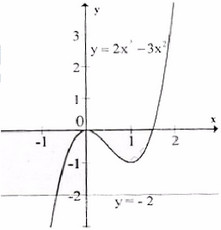
c) Xét hàm số y = f(x) = 2x2 - 2x4. Tập xác định : R.
y' = 4x - 4x3 = 4x(1 - x2); y' = 0 ⇔ x = 0,x = ±1.
Bảng biến thiên:
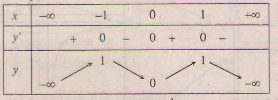
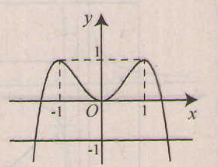
Đồ thị hàm số f(x) và đường thẳng y = -1 như hình bên.
Từ đồ thị ta thấy phương trình đã cho có hai nghiệm phân biệt.
BB
1
29 tháng 3 2016
Đặt \(t=2^x\left(t>0\right)\) thì phương trình trở thành
\(4t^2-2t.4-\left(t^4+2t^3\right)=0\)
Bây giờ coi 4=u là một ẩn của phương trình, còn t là số đã biết. Phương trình trở thành phương trình bậc 2 đối với ẩn u. Tính \(\Delta'\)
ta có :
\(\Delta'=\left(-t\right)^2+\left(t^4+2t^3\right)=\left(t^2+t\right)^2\)
Do đó :
\(\begin{cases}u=t-t\left(t+1\right)\\u=t+t\left(t+1\right)\end{cases}\) \(\Leftrightarrow\begin{cases}4=-t^2\\4=t^2+2t\end{cases}\) \(\Leftrightarrow t^2+2t-4=0\)
\(\Leftrightarrow\begin{cases}t=-1-\sqrt{5}\\t=-1+\sqrt{5}\end{cases}\)
Suy ra \(2^x=\sqrt{5}-1\Leftrightarrow x=\log_2\left(\sqrt{5}+1\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 6 2019
a/ ĐKXĐ: \(x>\frac{1}{2}\)
\(\Leftrightarrow\frac{3x^2-1}{\sqrt{2x-1}}-\sqrt{2x-1}=mx\)
\(\Leftrightarrow\frac{3x^2-2x}{\sqrt{2x-1}}=mx\Leftrightarrow\frac{3x-2}{\sqrt{2x-1}}=m\)
Đặt \(\sqrt{2x-1}=a>0\Rightarrow x=\frac{a^2+1}{2}\Rightarrow\frac{3a^2-1}{2a}=m\)
Xét hàm \(f\left(a\right)=\frac{3a^2-1}{2a}\) với \(a>0\)
\(f'\left(a\right)=\frac{12a^2-2\left(3a^2-1\right)}{4a^2}=\frac{6a^2+2}{4a^2}>0\)
\(\Rightarrow f\left(a\right)\) đồng biến
Mặt khác \(\lim\limits_{a\rightarrow0^+}\frac{3a^2-1}{2a}=-\infty\); \(\lim\limits_{a\rightarrow+\infty}\frac{3a^2-1}{2a}=+\infty\)
\(\Rightarrow\) Phương trình đã cho luôn có nghiệm với mọi m
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 6 2019
b/ ĐKXĐ: \(x\ge2\)
\(\Leftrightarrow\sqrt[4]{\left(x-1\right)^2}+4m\sqrt[4]{\left(x-1\right)\left(x-2\right)}+\left(m+3\right)\sqrt[4]{\left(x-2\right)^2}=0\)
Nhận thấy \(x=2\) không phải là nghiệm, chia 2 vế cho \(\sqrt[4]{\left(x-2\right)^2}\) ta được:
\(\sqrt[4]{\left(\frac{x-1}{x-2}\right)^2}+4m\sqrt[4]{\frac{x-1}{x-2}}+m+3=0\)
Đặt \(\sqrt[4]{\frac{x-1}{x-2}}=a\) pt trở thành: \(a^2+4m.a+m+3=0\) (1)
Xét \(f\left(x\right)=\frac{x-1}{x-2}\) khi \(x>0\)
\(f'\left(x\right)=\frac{-1}{\left(x-2\right)^2}< 0\Rightarrow f\left(x\right)\) nghịch biến
\(\lim\limits_{x\rightarrow2^+}\frac{x-1}{x-2}=+\infty\) ; \(\lim\limits_{x\rightarrow+\infty}\frac{x-1}{x-2}=1\) \(\Rightarrow f\left(x\right)>1\Rightarrow a>1\)
\(\left(1\right)\Leftrightarrow m\left(4a+1\right)=-a^2-3\Leftrightarrow m=\frac{-a^2-3}{4a+1}\)
Xét \(f\left(a\right)=\frac{-a^2-3}{4a+1}\) với \(a>1\)
\(f'\left(a\right)=\frac{-2a\left(4a+1\right)-4\left(-a^2-3\right)}{\left(4a+1\right)^2}=\frac{-4a^2-2a+12}{\left(4a+1\right)^2}=0\Rightarrow a=\frac{3}{2}\)
\(f\left(1\right)=-\frac{4}{5};f\left(\frac{3}{2}\right)=-\frac{3}{4};\) \(\lim\limits_{a\rightarrow+\infty}\frac{-a^2-3}{4a+1}=-\infty\)
\(\Rightarrow f\left(a\right)\le-\frac{3}{4}\Rightarrow m\le-\frac{3}{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 8 2020
3.
- Với \(m=1\Rightarrow f\left(x\right)=-9x\) nghịch biến trên R (ko thỏa mãn)
- Với \(m=-1\Rightarrow f\left(x\right)=9x\) đồng biến trên R (thỏa mãn)
- Với \(m\ne\pm1\)
\(f'\left(x\right)=6\left(m^2-1\right)x^2-9m\ge0;\forall x>1\)
TH1: \(\left\{{}\begin{matrix}m^2-1>0\\m\left(m^2-1\right)\le0\end{matrix}\right.\) \(\Rightarrow m< -1\)
TH2: \(\left\{{}\begin{matrix}m^2-1>0\\m\left(m^2-1\right)>0\\x_1< x_2\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2-1>0\\m\left(m^2-1\right)>0\\\sqrt{\frac{3m}{2\left(m^2-1\right)}}\le1\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\3m\le2m^2-2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>1\\2m^2-3m-2\ge0\end{matrix}\right.\)
\(\Rightarrow m\ge2\)
Vậy \(\left[{}\begin{matrix}m\le-1\\m\ge2\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 8 2020
2.
\(\Leftrightarrow y'=2m-\frac{x+1}{\sqrt{x^2+2x+11}}\ge0;\forall x\in R\)
\(\Leftrightarrow2m\ge\frac{x+1}{\sqrt{x^2+2x+11}}\)
\(\Leftrightarrow m\ge\frac{x+1}{2\sqrt{x^2+2x+11}}\)
\(\Leftrightarrow m\ge\max\limits_Rf\left(x\right)\) với \(f\left(x\right)=\frac{x+1}{2\sqrt{x^2+2x+11}}\)
Ta có: \(f'\left(x\right)=\frac{5}{\sqrt{\left(x^2+2x+11\right)^3}}>0;\forall x\)
\(\Rightarrow f\left(x\right)\) đồng biến trên R
\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow+\infty}\frac{x+1}{2\sqrt{x^2+2x+11}}=\frac{1}{2}\)
\(\Rightarrow f\left(x\right)< \frac{1}{2};\forall x\in R\)
\(\Rightarrow m\ge\frac{1}{2}\)
\(3x^2+2x-1=0\)
\(\Rightarrow3x^2+3x-x-1=0\)
\(\Rightarrow3x.\left(x+1\right)-\left(x+1\right)=0\)
\(\Rightarrow\left(x+1\right).\left(3x-1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x+1=0\\3x-1=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-1\\3x=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-1\\x=\dfrac{1}{3}\end{matrix}\right.\)
Vậy \(x\in\left\{-1;\dfrac{1}{3}\right\}\)
Chúc bạn học tốt nha!!!
Em làm bài này không chắc lắm! Nếu sai thì em xin lỗi anh Hoàng nha! Chưa thấy ai làm em làm đó nha!!!
Bài làm:
\(3x^2+2x-1=0\\ < =>x^2+2x^2+2x+1-2=0\\ < =>\left(x^2+2x+1\right)+\left(2x^2-2\right)=0\\ < =>\left(x+1\right)^2+2\left(x-1\right)\left(x+1\right)=0\\ < =>\left(x+1\right)\left(x+1+2\left(x-1\right)\right)=0\\ < =>\left(x+1\right)\left(x+1+2x-2\right)=0\\ < =>\left(x+1\right)\left(3x-1\right)=0\\ =>\left[{}\begin{matrix}x+1=0\\3x-1=0\end{matrix}\right.< =>\left[{}\begin{matrix}x=-1\\x=\dfrac{1}{3}\end{matrix}\right.\)