Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tóm tắt:
m = 12 kg
C = 460 J/kg.K
t0 = 20oC
Q = 44160J
t = ?
Giải:
Nhiệt độ của thỏi thép sau khi nhận nhiệt lượng:
Q = m.c(t − t0)
→ t = t0 + Q/mc = 15 + 44160/12.460 = 28oC
Ơ cái này phải là nhiệt độ của nó tăng lên bao nhiêu mà :))??
Nhiệt độ của thỏi thép là
\(Q=mc\Delta t\\ =12.460\left(t-15\right)=44160\\ \Rightarrow t=23^o\)

Qthu = Qtoả
2.4200.(x-40) = 0,3.460(80-x)
=> 8400x-336000 = 11040 - 138x
=> 8538x = 347040
=> x = 40,65
Vậy nước sẽ nóng thêm: 40,65 - 40 = 0,65 độ
\(m_1=0,3kg\\ t_1=80^oC\\ m_2=2kg\\ t_2=40^oC\\ c_2=4200J/kg.K\\ c_1=460J/kg.K\\ \Delta t_2=?\)
GIẢI
Nhiệt lượng quả cầu tỏa ra là:
\(Q_1=m_1.c_1.\left(t_1-t\right)=0,3.460.\left(80-t\right)\left(J\right)\)
Nhiệt lượng nước thu vào là:
\(Q_2=m_2.c_2.\left(t-t_2\right)=2.4200.\left(t-40\right)\left(J\right)\)
Theo phương trình cân bằng nhiệt:
\(Q_{tỏa}=Q_{thu}\\ \Rightarrow Q_1=Q_2\\ \Rightarrow0,3.460.\left(80-t\right)=2.4200.\left(t-40\right)\\ \Rightarrow11040-138t=8400t-336000\\ \Rightarrow8400t+138t=11040+336000\\ \Rightarrow8538t=347040\\ \Rightarrow t=\dfrac{347040}{8538}\approx40,65\left(^oC\right)\\ \Rightarrow\Delta t_2=40,65-40=0,65\left(^oC\right)\)
Vậy nước nóng thêm 0,65oC khi có cân bằng nhiệt.

\(m=5kg\)
\(t_1=25^oC;t_2=26^oC\)
\(\Rightarrow\Delta t=t_2-t_1=26-25=1^oC\)
\(c=460J/kg.K\)
\(Q=?J\)
======================
Nhiệt lượng cần truyền là :
\(Q=m.c.\Delta t=5.460.1=2300\left(J\right)\)
Nhiệt lượng cần truyền cho thép :
\(Q=c.m.\Delta t=460.5.1=2300\left(J\right)\)

a) khối thép thu nhiệt do tăng nhiệt độ
b) Nhiệt lương cần truyền cho khối thép
`Q = mc*(t_2-t_1) = 2*460*(250-20)=211600(J)`

Tóm tắt:
t1 = 345oC
c1 = 460J/KgK
m2 = 3kg
t2 = 25oC
c2 = 4200J/KgK
to = 33oC
m1 = ?
------------------------------------
Nhiệt lượng thu vào của nước là:
Qthu = \(m_1\cdot c_1\cdot\left(t^o-t_2\right)\)
= \(3\cdot4200\cdot\left(33-25\right)\)
= 100800 (J)
Theo phương trình cân bằng nhiệt:
Qthu = Qtỏa = 100800J
Qtỏa = \(m_1\cdot c_1\cdot\left(t_1-t^o\right)\)
100800J = \(m_1\cdot460\cdot\left(345-33\right)\)
=> m1 = \(\dfrac{100800}{460\cdot\left(345-33\right)}\) = 0,7 (kg)

Tóm tắt
\(t_1=260^0C\)
\(c_1=\) 460 J/Kg.K
\(t_2=20^0C\)
\(c_2=\) 4200 J/Kg.K
\(m_2=2kg\)
\(t=50^0C\)
a) \(Q=?J\) ; b) \(m_1=?kg\)
Giải
Nhiệt lượng thu vào của nước là:
\(Q_2=m_2\cdot c_2\cdot\left(t-t_2\right)=2\cdot4200\cdot\left(50-20\right)=252000\left(J\right)\)
Nhiệt lượng của quả cầu bằng nhiệt lượng của nước thu vào
\(Q_1=Q_2=252000\left(J\right)\)
Khối lượng của quả cầu là
\(Q_1=m_1\cdot c_1\cdot\left(t_1-t\right)\)
\(\Rightarrow m_1=\dfrac{Q_1}{c_1\cdot\left(t_1-t\right)}\)
\(\Rightarrow m_1=\dfrac{252000}{460\cdot\left(260-50\right)}=2,6\left(kg\right)\)
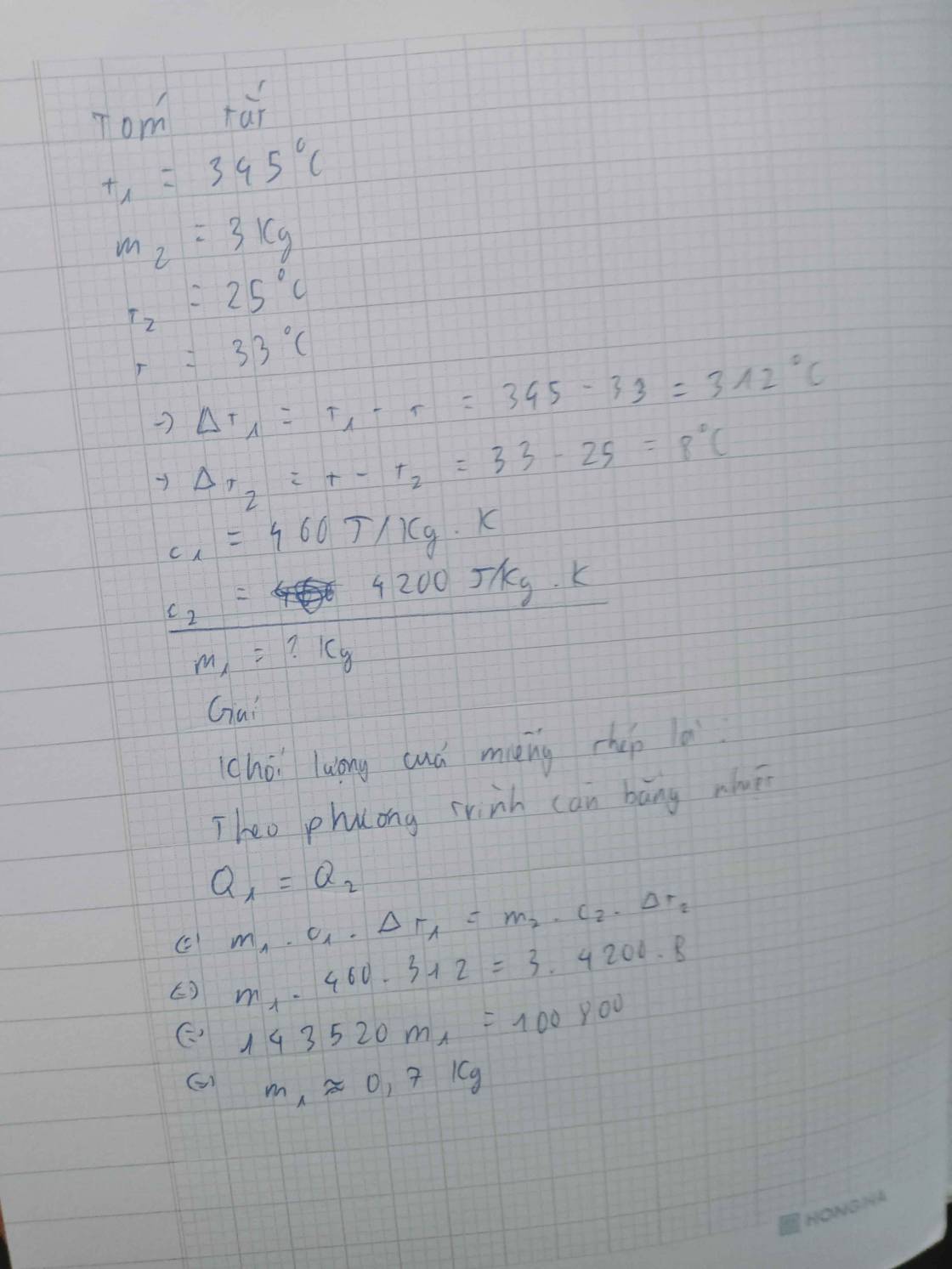
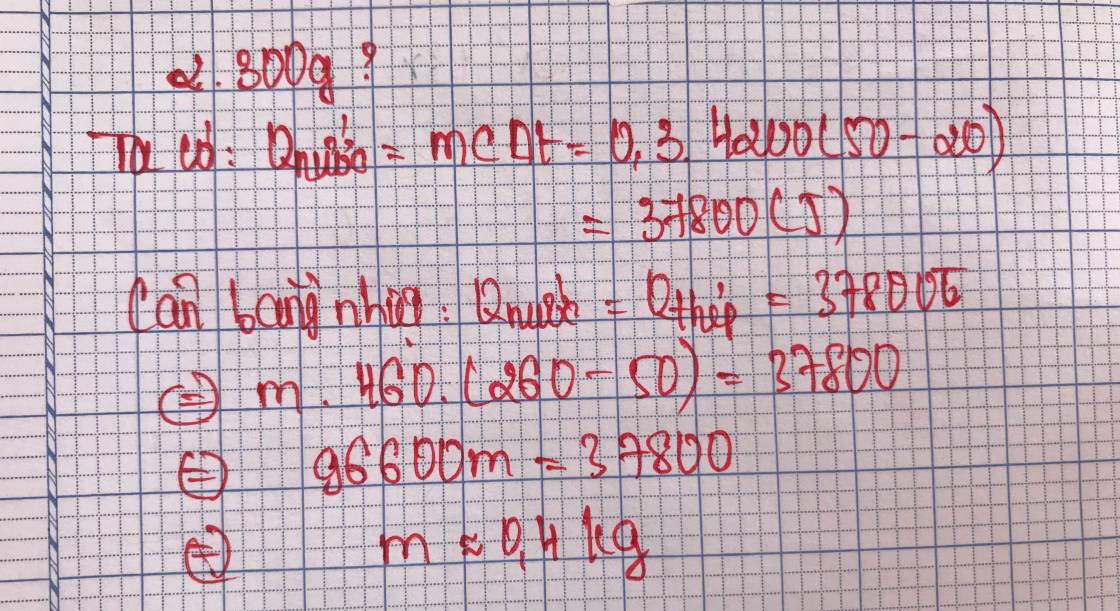
Tóm tắt:
\(m=12kg\)
\(t_1=20^oC\)
\(c=460J/kg.K\)
\(Q=44160J\)
============
\(\Delta t=?^oC\)
Nhiệt độ mà miếng thép tăng lên:
\(Q=m.c.\Delta t\Rightarrow\Delta t=\dfrac{Q}{m.c}=\dfrac{44160}{12.460}=8^oC\)
Vậy nhiệt độ của thỏi thép khi tăng lên:
\(\Delta t=t_2-t_1\Rightarrow t_2=\Delta t+t_1=8+20=28^oC\)