Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

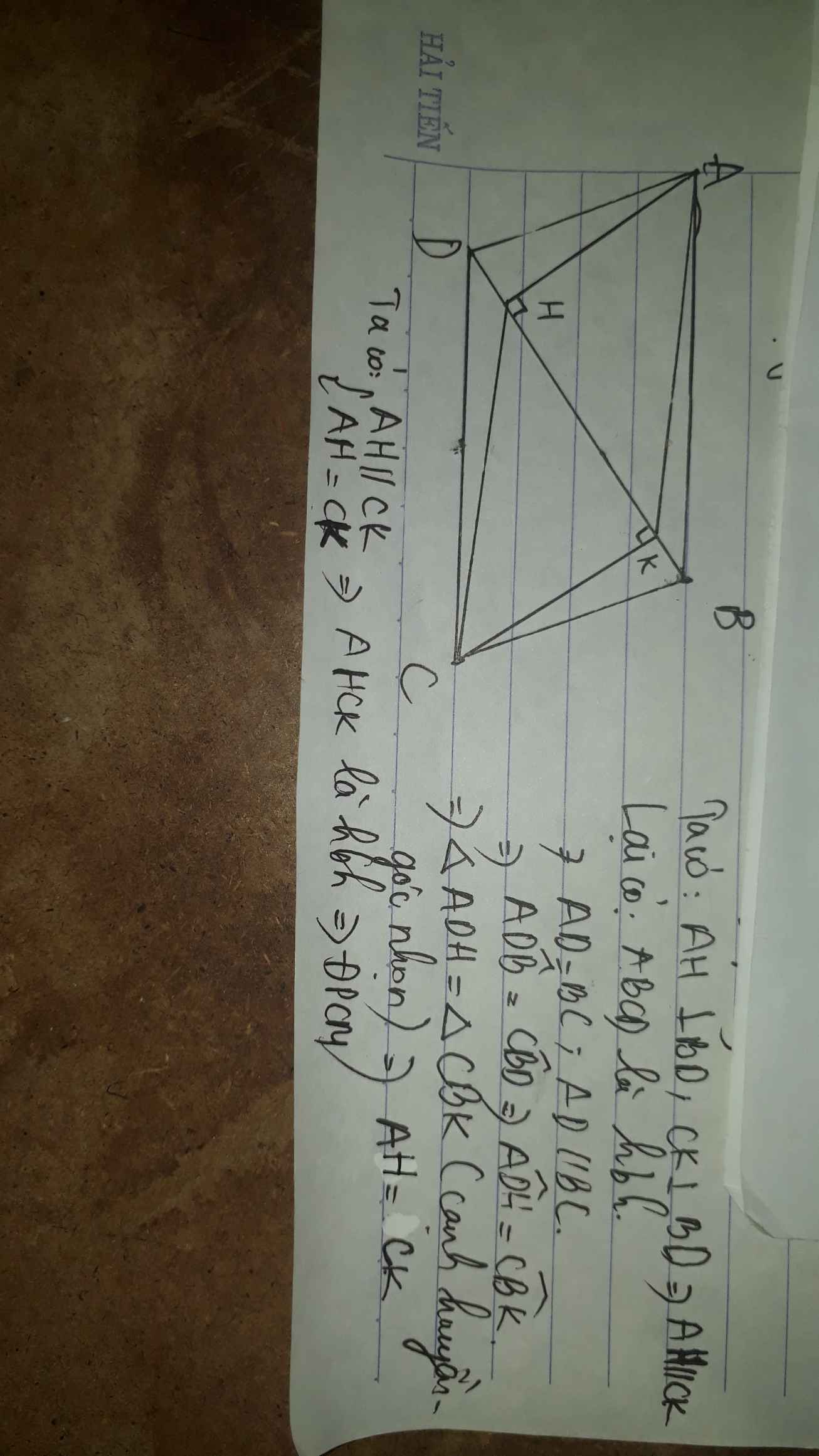
có tam giác ABD=BCD (c.c.c) suy ra CK=AH a b c d h k
xét tứ giác AKCH có ck=ah cmt hkc=ahk=90 độ ( so le trong ) -> ah//kc -> AKCH là hình bình hành (dhnb)-> CH=AK
xét tam giác ADK và BCH có BC=AD CH=AK cmt có góc ADH= góc CBK so le trong -> ADK=BCH (c.g.c)
xét tam giác ABH VÀ CKH = nhau (c.g.c) ( chứng minh tượng tự ) -
Ta có đa giác ABCH = AHB+CHD và ADCK=AKD+CKD MÀ AHB=Ckd cmt . ADK = BCH cmt -> tứ giác ABCH=ADCK-> diện tích=nhau

Ta có:
△ ABC = △ ADC (c.c.c) ⇒ S A B C = S A D C (1)
△ AHC = △ AKC (c.c.c) ⇒ S A H C = S A K C (2)
Từ (l) và (2) ⇒ S A B C + S A H C = S A D C + S A K C
Hay S A B C H = S A D C K

có tam giác ABD=BCD (c.c.c) suy ra CK=AH
xét tứ giác AKCH có ck=ah cmt hkc=ahk=90 độ ( so le trong )
-> ah//kc -> AKCH là hình bình hành (dhnb)
-> CH=AK xét tam giác ADK và BCH có BC=AD CH=AK cmt có góc ADH= góc CBK so le trong
-> ADK=BCH (c.g.c) xét tam giác ABH VÀ CKH = nhau (c.g.c)-> diện tích=nhau
( chứng minh tượng tự ) - Ta có đa giác ABCH = AHB+CHD
và ADCK=AKD+CKD MÀ AHB=Ckd cmt . ADK = BCH cmt
-> tứ giác ABCH=ADCK
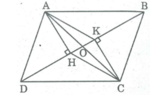
A D B C H K 1 2 2 1
Xét 2 tam giác vuông HDA và KBC có :
AD = BC ( ABCD - hbh )
\(\widehat{D1}=\widehat{B1}\)( so le trong , AD // Bc )
\(\Rightarrow\)\(\Delta HDA=\Delta KBC\)( ch-gn )
\(\Rightarrow\)Diện tích tam giác HDA = diện tích tam giác KBC ( 1 )
Xét t/g HDC và t/g KBA :
CD = AB ( gt )
\(\widehat{D2}=\widehat{B2}\)( so le trong , CD // AB )
HD = KB ( t/g HDA = t/g KBC )
\(\Rightarrow\)\(\Delta HDC=\Delta KBA\)( c-g-c )
\(\Rightarrow\)Diện tích tam giác HDC = diện tích tam giác KBA ( 2 )
Diện tích ABCH = diện tích KBA + diện tích AK Ch + diện tích KBC ( 3 )
Diện tích ADCK = diện tích HDC + diện tích AKCH + diện tích HDA ( 4 )
Từ ( 1 ) ; ( 2 ) ; ( 3 ) : ( 4 ) suy ra diện tích đa giác ABCH = diện tích ADCK ( đpcm )

Xét ΔAED vuông tại E và ΔCFB vuông tại F có
AD=CB(Hai cạnh đối của hình bình hành ABCD)
\(\widehat{D}=\widehat{B}\)(Hai góc đối của hình bình hành ABCD)
Do đó: ΔAED=ΔCFB(cạnh huyền-góc nhọn)
Suy ra: AE=CF(Hai cạnh tương ứng) và ED=FB(hai cạnh tương ứng)
Ta có: ED+EC=DC(E nằm giữa D và C)
FB+FA=AB(F nằm giữa A và B)
mà AB=DC(Hai cạnh đối của hình bình hành ABCD)
và ED=FB(cmt)
nên EC=FA
Xét tứ giác ECFA có
EC=FA(cmt)
EA=CF(cmt)
Do đó: ECFA là hình bình hành(Dấu hiệu nhận biết hình bình hành)

a) Chứng minh các cặp tam giác bằng nhau:
DABH = DCDK và DBCH = DDAK
Từ đó, suy ra AABH + SBCH = SCDH + SDAK
Þ ĐPCM.
b) Trừ cả 2 vế của ý a) cho SAKCH, ta thu được SABCK = SADCH


Ta chứng minh AH//CK, AH = CK (DAHD = DCKB) Þ AHCK là hình bình hành (cặp cạnh đối song song và bằng nhau)