Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔBAC nội tiếp
AC là đường kính
Do đó: ΔBAC vuông tại B
Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{BAC}=\dfrac{1}{2}\cdot sđ\stackrel\frown{BC}=\dfrac{1}{2}\cdot60^0=30^0\)
Gọi H là giao điểm của BD với AC
BD\(\perp\)AC nên BD\(\perp\)AC tại H
ΔOBD cân tại O
mà OH là đường cao
nên H là trung điểm của BD
Xét ΔCBD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCBD cân tại C
=>CB=CD
Xét ΔCOD và ΔCOB có
CD=CB
OD=OB
CO chung
Do đó: ΔCOD=ΔCOB
=>\(\widehat{COD}=\widehat{COB}\)
=>\(sđ\stackrel\frown{CB}=sđ\stackrel\frown{CD}=60^0\)
Xét ΔBAC vuông tại B có \(\widehat{BAC}+\widehat{BCA}=90^0\)
=>\(\widehat{BCA}+30^0=90^0\)
=>\(\widehat{BCA}=60^0\)
Xét (O) có
\(\widehat{BCA}\) là góc nội tiếp chắn cung AB
Do đó: \(\widehat{BCA}=\dfrac{1}{2}\cdot sđ\stackrel\frown{AB}\)
=>\(sđ\stackrel\frown{AB}=2\cdot\widehat{BCA}=120^0\)
DF//AC
DB\(\perp\)AC
Do đó: DF\(\perp\)DB
=>ΔDFB vuông tại D
ΔDFB vuông tại D
nên ΔDFB nội tiếp đường tròn đường kính BF
mà ΔDFB nội tiếp (O)
nên O là trung điểm của BF
=>OA//DF
=>\(\widehat{BFD}=\widehat{BOH}=\widehat{BOC}\)(hai góc đồng vị)
=>\(\widehat{BFD}=60^0\)
ΔBDF vuông tại D
=>\(\widehat{BFD}+\widehat{FBD}=90^0\)
=>\(\widehat{FBD}+60^0=90^0\)
=>\(\widehat{FBD}=30^0\)
Xét (O) có
\(\widehat{FBD}\) là góc nội tiếp chắn cung FD
Do đó: \(\widehat{FBD}=\dfrac{1}{2}\cdot sđ\stackrel\frown{FD}\)
=>\(sđ\stackrel\frown{FD}=2\cdot\widehat{FBD}=2\cdot\)30=60 độ

a) Điểm C nằm trên cung nhỏ AB ( hình a)
Số đo cung nhỏ BC = 100º – 45º = 55º
Số đo cung lớn BC = 360º – 55º = 305º
b) Điểm C nằm trên cung lớn AB (hình b)
Số đo cung nhỏ BC = 100º + 45º = 145º
Số đo cung lớn BC = 360º – 145º = 215º
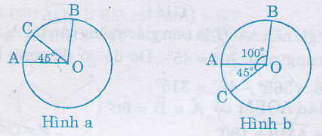

a) Ta có \(\widehat{AND}=\widehat{AMD}\)(góc nội tiếp cùng chắn cung AD)
\(AM//BN\Rightarrow\widehat{AMN}=\widehat{MNB}\left(slt\right)\)
Ta có góc ANB nội tiếp đường trong O chắn nửa đường trong => góc ANB=900
Ta có: \(\widehat{AMD}+\widehat{AMN}+\widehat{DNM}=\widehat{DNM}+\widehat{AND}+\widehat{MNB}\)
\(\Leftrightarrow\widehat{DMN}+\widehat{MND}=90^0\Leftrightarrow\widehat{NDM}=90^0\)
Vì DM//AB và ND vuông góc với DM => DN vuông góc với AB
b) Ta có \(\widehat{BAN}=\widehat{BMN}\)(cùng chắn cung BN)
Mà \(\widehat{AMN}+\widehat{NMB}=90^0\Rightarrow\widehat{BAN}+\widehat{BAM}=90^0\Rightarrow\widehat{MAN}=90^0\)
\(\Rightarrow MANB\)là hcn
=> AM=BN
Ta có MC//AE và AM//EC => AMCE là hbh => AM=EC mà AM=BN => BN=EC mà BN//EC => ENBC là hbh =>EN//CB => CB vuông góc với AB(vì AB vuông góc với EN)=> BC là tiếp tuyến của đường tròn O
Chúc bạn học tốt!!!