Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề bài ta có :
Lúc đi:
147x+105y+126z=17640(1)
Khi về do hướng đi ngược lại nên đoạn lên dốc và xuống dóc sẽ đổi cho nhau : x,y lần lượt là đoạn xuống dốc và đoạn lên dốc . Ta có :
105x+147y+126z=26460(2)
Lấy (1)+(2) Ta rút gọn nên được :

Tham khảo:
a) Đổi: 1 giờ 30 phút = 1,5 giờ; 15 phút = 0,25 giờ; t phút = \(\frac{t}{{60}}\) giờ
Nếu \(t \le 90\)(phút) thì quãng đường s mà người đó đi được là: \(42.\frac{t}{{60}} = 0,7t\)(km)
Nếu \(90 < t \le 90 + 15 = 105\)(phút) thì quãng đường s mà người đó đi được là: \(42.1,5 = 63\)(km)
Nếu \(105 < t \le 105 + 120 = 225\)(phút) thì quãng đường s mà người đó đi được là: \(42.1,5 + (\frac{t}{{60}} - 1,5 - 0,25).30 = 0,5t + 10,5.\)(km)
Như vậy hàm số tính quãng đường s (km) sau t phút là:
\(s = \left\{ \begin{array}{l}0,7t\quad \quad \quad \quad (0 \le t \le 90)\\63\quad \quad \quad \quad \;\;\;(90 < t \le 105)\\0,5t + 10,5\quad \;\;(105 < t \le 225)\end{array} \right.\)
b)
Với \(0 \le t \le 90\) thì \(s = 0,7t\)
Trên đoạn [0;90] ta vẽ đường thẳng \(s = 0,7t\)
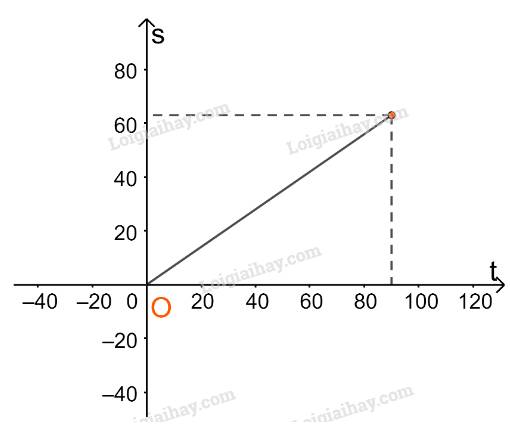
Với \(90 < t \le 105\) thì \(s = 63(km)\)
Trên nửa khoảng (90;105] ta vẽ đường thẳng \(s = 63\)
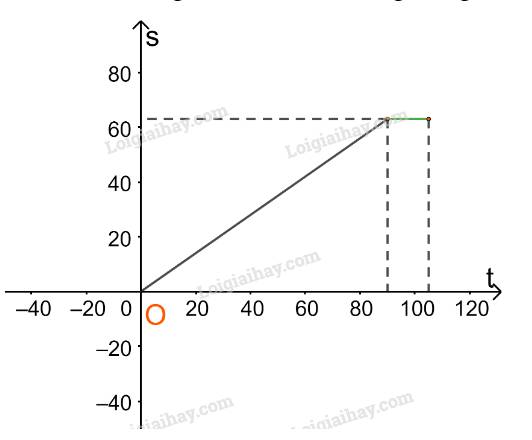
Với \(105 < t \le 225\)(phút) thì \(s = 0,5t + 10,5.\)(km)
Trên nửa khoảng (105;225] ta vẽ đường thẳng \(s = 0,5t + 10,5.\)
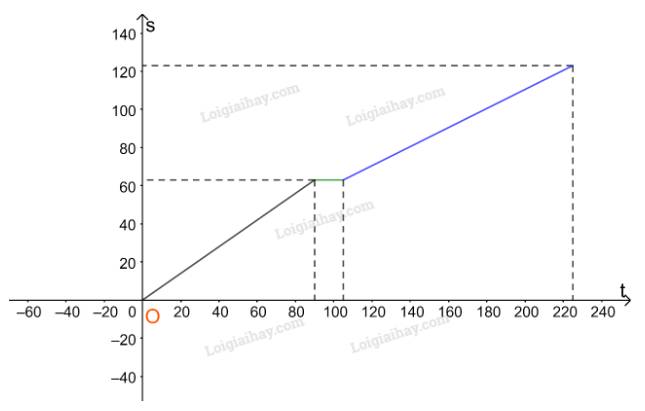
Như vậy ta được đồ thị biểu diễn hàm số s theo t như hình trên.

Thời gian để ô tô gặp xe máy là:
132.8:(48+35)=8/5 (giờ)=96 (phút)=1 giờ 36 phút
ĐS:1 giờ 36 phút
