Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn lập tỉ số giữa H1 và H2
H1=1-R.P/U12
H2=1-R.P/U22
bạn chuyển vế rồi lập tỉ số vì R và P như nhau nên rút gọn
=>(1-H1)/(1-H2)=U22/U12
=>(1-0,84)/(1-0,96)=U22/102
=>U2=20kV
Chắc đúng hì
Hiệu suất từ 84% tăng lên 96% có nghĩa hao phí từ 16% giảm xuống 4% (giảm đi 4 lần)
Mà \(\Delta P =\dfrac{P^2.R}{U^2\cos^2\varphi}\)
Nên để \(\Delta P\) giảm 4 lần thì U tăng 2 lần, có giá trị là: \(10.2 = 20kV\)

Đáp án A
Cách giải:
Công suất nơi phát là: P
Công suất tiêu thụ của mỗi hộ dân là P0
+ Nếu tăng điện áp hiệu dụng nơi phát từ U lên 2U thì số hộ dân có đủ điện để tiêu thụ tăng từ 80 hộ lên 95 hộ
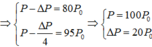
Sợi dây siêu dẫn có R = 0 => DP = 0 => P = 100P0 => số hộ dân đủ điện để tiêu thụ là 100 hộ

Bài này chỉ cần sử dụng công thức 2 giá trị của C để có cùng 1 giá trị của $U_C$ :
$U_C=U_{C_{max}} \cos \left(\dfrac{\varphi _1-\varphi _2}{2} \right)$
$\Rightarrow U_{C_{max}}=\dfrac{60}{\cos \dfrac{\pi }{6}}=40\sqrt{3} V$
Khi $U_{C_{max}}$ ta có:
$P=\dfrac{U^2}{R}\cos ^2\varphi _3=P_{max}\cos ^2\varphi _3=\dfrac{P_{max}}{2}$
$\Rightarrow \cos \varphi _3=\dfrac{\sqrt{2}}{2}$
Vẽ giản đồ suy ra: $U=\dfrac{U_{C_{max}}}{\sqrt{2}}=20\sqrt{6}\left(V \right)$

Áp dụng: \(\dfrac{2}{L_0}=\dfrac{1}{L_1}+\dfrac{1}{L_2}\)
Suy ra \(L_0=\dfrac{3}{2\pi}(H)\)

C thay đổi để Uc max thì điện áp uRL vuông pha với u. Ta có giản đồ véc tơ sau:
i U U U=30 O M N J RL C U = 32 L
Xét tam giác vuông OMN:
\(ON^2=NJ.NM\Rightarrow 30^2=(U_C-32).U_C\)
\(\Rightarrow U_C^2-32U_C-30^2=0\)
Giải PT ta được \(U_C=50V\)
Chọn D.
Đặt một điện áp xoay chiều với giá trị hiệu dụng U= 30V vào hai đầu đoạn mạch R, L, C mắc nối tiếp có điện dung C thay đổi được. Khi điện áp hiệu dụng giữa hai bản tụ điện đạt giá trị cực đại UCmax thì hiệu điện thế hiệu dụng giữa hai đầu cuộn cảm là UL = 32V. Giá trị UCmax là
A. 18V
B. 25V
C. 40V
D. 50V

Chọn đáp án C
+ Công suất tiêu thụ không đổi nên: ![]()
+ Hệ số công suất của cuộn dây: ![]()

trạm phát tiêu thụ
Công suất hao phí trong quá trình truyền đi là \(\Delta P = \frac{P^2}{U^2}R.(1)\)
=> \(H_1 = 1 - \frac{\Delta P_1}{P} =1 - \frac{P}{U_1^2}R.\)
\(H_2 = 1 - \frac{\Delta P_2}{P} =1 - \frac{P}{U_2^2}R.\)
Mà \(U_1 = 20kV; U_2 = 20+10 = 30kV.\)
=> \(\frac{1-H_1}{1-H_2} = \frac{U_2^2}{U_1^1} = \frac{9}{4}=> 4-4H_1 = 9-9H_2 \)
=> \(H_2 = \frac{5+4H_1}{9} = \frac{5+4.0,82}{9}=0,92 = 92\%.\)
Chọn đáp án.D