Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

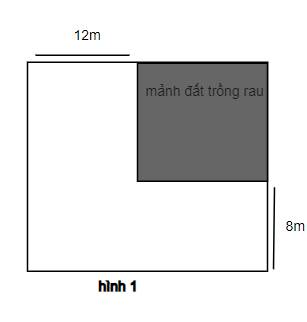
Chiều dài của mảnh đất trồng rau: \(x-8\) (m)
Chiều rộng của mảnh đất trồng rau: \(x-12\left(m\right)\)
Diện tích của mảnh đất trồng rau: \(\left(x-8\right)\left(x-12\right)\left(m^2\right)\)
Ta có phương trình:
\(\left(x-8\right)\left(x-12\right)=96\)
\(\Leftrightarrow x^2-8x-12x+84=96\)
\(\Leftrightarrow x^2-20x+96-96=0\)
\(\Leftrightarrow x^2-20x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=20\left(tm\right)\end{matrix}\right.\)
Vậy độ dài của khu vườn là 20 m

a) Vì tam giác ABC vuông tại A
=> BAC = 90 độ
=> Vì K là hình chiếu của H trên AB
=> HK vuông góc với AB
=> HKA = 90 độ
=> HKA = BAC = 90 độ
=> KH // AI
=> KHIA là hình thang
Mà I là hình chiếu của H trên AC
=> HIA = 90 độ
=> HIA = BAC = 90 độ
=> KHIA là hình thang cân
b) Vì KHIA là hình thang cân
=> KA = HI
= >KI = HA
Xét tam giác KAI vuông tại A và tam giác HIC vuông tại I có
KA = HI
KI = AH
=> Tam giác KAI = tam giác HIC ( cgv-ch)
=> KIA = ACB ( DPCM)
c) con ý này tớ nội dung chưa học đến thông cảm

Giải:
a, đa thức tính diện tích mảnh đất trồng rau là:
S = \(x.x\) (m2)
S = \(x^2\) (m2)
b,Theo bài ra ta có: \(x^2\) = 96
\(\) \(\left[{}\begin{matrix}x=4\sqrt{6}\\x=-4\sqrt{6}\end{matrix}\right.\)
Vì \(x\) > 0 nên \(x\) = 4\(\sqrt{6}\)
Kết luận: cạnh của khu vườn có độ dài là: 4\(\sqrt{6}\)(m)

a. Xét tam giác HCD cóHN=DN;HM=CM
=> MN là đường trung bình của tam giác HCD => MN//DC
=> DNMC là hình thang
b. Ta có MN là đường trung bình của tam giác HCD => MN=1/2CD
Mà AB=1/2CD => AB =MN
Do MN//CD và AB//CD => AB//MN
Xét tứ giác ABMN có AB//MN; AB=MN
=> ABMN là hình bình hành
c.Ta có MN//CD mà CD vg AD
=> MN vg AD
Xét tam giác ADM có DH và MN là 2 đường cao của tam giác
Mà chúng cắt nhau tại N nên N là trực tâm của tam giác ADM
=> AN là đường cao của tam giác ADM
=> AN vg DM
Do ABMN là hình bình hành nên AN//BM
=> BM vg DM => BMD =90*

a) BD, CE là các đường trung tuyến của \(\Delta ABC\)
\(\Rightarrow\)DA = DC; EA =EB
\(\Rightarrow\)ED là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\)ED // BC; ED = 1/2 BC
\(\Delta GBC\)có MG = MB; NG = NC
\(\Rightarrow\)MN là đường trung bình của \(\Delta GBC\)
\(\Rightarrow\)MN // BC; MN = 1/2 BC
suy ra: MN // ED; MN = ED
\(\Rightarrow\)tứ giác MNDE là hình bình hành
c) MN = ED = 1/2 BC
\(\Rightarrow\)MN + ED = \(\frac{BC}{2}\)+ \(\frac{BC}{2}\)= BC
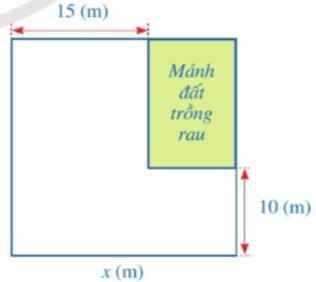
Chiều rộng mảnh đất trồng rau là x-15(m)
Chiều dài mảnh đất trồng rau là x-10(m)
Theo đề, ta có:
(x-15)(x-10)=475
=>\(x^2-25x+150-475=0\)
=>\(x^2-25x-325=0\)
=>\(\left[{}\begin{matrix}x=\dfrac{25+5\sqrt{77}}{2}\left(nhận\right)\\x=\dfrac{25-5\sqrt{77}}{2}\left(loại\right)\end{matrix}\right.\)
Vậy: \(x=\dfrac{25+5\sqrt{77}}{2}\left(m\right)\)