Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có:
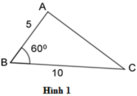
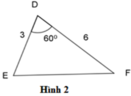
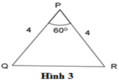
B A B C = 5 10 = 1 2 ; D E D F = 3 6 = 1 2 ; P Q P R = 4 4 = 1 ⇒ B A B C = D E D F = 1 2
Xét ΔABC và ΔEDF ta có:
B A B C = D E D F (cmt) ⇔ D E B A = D F B C
B = D = 60 ∘ (gt)
=> ΔABC ~ ΔEDF (c - g - c).
Đáp án: A

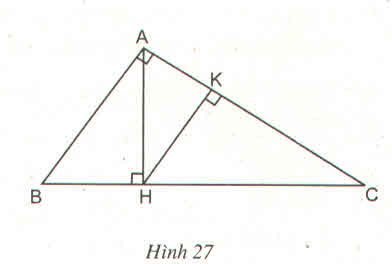
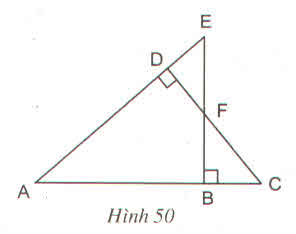
∆ADC ∽ ∆ABE vì góc A chung và \(\widehat{D}\)= \(\widehat{B}\) = 900
∆DEF ∆BCF vì \(\widehat{D}\) = \(\widehat{B}\) = 900 , \(\widehat{DEF}=\widehat{BFC}\)
∆DFE ∆BAE vì ( \(\widehat{D}=\widehat{B}\) = 900 , góc A chung)
∆BFC ∆DAC vì (\(\widehat{D}=\widehat{B}\) = 900, góc C chung)

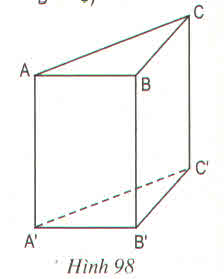
a) Những cặp mặt phẳng song song nhau: (ABC) // (A'B'C')
b) Những cặp mặt phẳng vuông góc với nhau: (ABB'A') ⊥ (A'B'C); (ACC'A') ⊥ (A'B'C'); (BCC'B') ⊥ (A'B'C); (ABB'A') ⊥ (ABC); (ACC'A') ⊥ (ABC); (BCC'B') ⊥ (ABC)
c) Điền vào ô trống:

a) MN // BC => ∆AMN ∽ ∆ABC
ML // AC => ∆MBL ∽ ∆ABC
và ∆AMN ∽ ∆MLB
b)
∆AMN ∽ ∆ABC có:
ˆAMNAMN^ = ˆABCABC^; ˆANMANM^ = ˆACBACB^
AMABAMAB= 1313
∆MBL ∽ ∆ABC có:
ˆMBLMBL^ = ˆBACBAC^, ˆBB^ chung, ˆMLBMLB^ = ˆACBACB^
MBABMBAB= 2323
∆AMN ∽ ∆MLB có:
ˆMANMAN^ = ˆBMLBML^, ˆAMNAMN^ = ˆMBLMBL^, ˆANMANM^ = ˆM
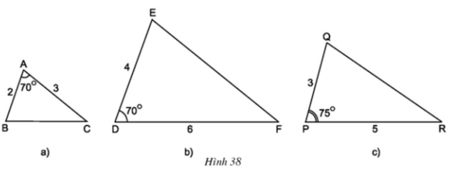









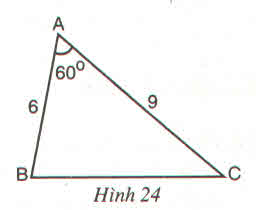


ΔABC và ΔDEF có
∠A = ∠D = 70o
⇒ ΔABC ∼ ΔDEF (c.g.c)